



suivant: 2.1.2 Paramétrages par des
monter: 2.1 Paramétrages
précédent: 2.1 Paramétrages
Table des matières
Un paramétrage d'une partie
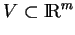 est une bijection
est une bijection  d'un ouvert
d'un ouvert 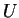 de
de
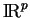 sur
sur  , de classe
, de classe 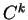 (2.1) dans
(2.1) dans 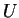 , de rang
, de rang 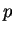 partout dans
partout dans 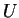 et dont la réciproque
et dont la réciproque
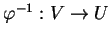 soit continue.
soit continue.
Voici un premier exemple de paramétrage. L'ensemble  est le complémentaire du pôle nord
est le complémentaire du pôle nord  de la sphère
de la sphère
Il associe à tout point
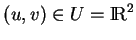 le point, différent de
le point, différent de 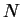 , en lequel la droite joignant
, en lequel la droite joignant 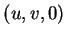 à
à 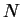 coupe
coupe  . On obtient facilement ses coordonnées
. On obtient facilement ses coordonnées
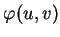 :
Ainsi,
:
Ainsi,  est de classe
est de classe 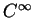 .
Posons, pour
.
Posons, pour 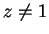 ,
L'application
,
L'application
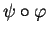 est l'identité dans
est l'identité dans
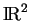 . En particulier, d'après la proposition 2,
. En particulier, d'après la proposition 2,
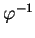 est continu. De plus, puisque
est continu. De plus, puisque
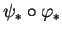 est injectif,
est injectif, 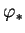 l'est aussi. Au total,
l'est aussi. Au total,
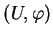 est un paramétrage.
est un paramétrage.
Nous venons d'utiliser une remarque très simple mais également très efficace. La voici formulée en termes généraux. Soient des applications 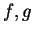 .
.
- -
- Si
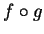 est injectif, alors
est injectif, alors 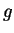 est injectif
est injectif
- -
- Si
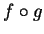 est surjectif, alors
est surjectif, alors  est surjectif
est surjectif
La vérification est facile. Ce serait une bonne idée de garder ces observations en mémoire.




suivant: 2.1.2 Paramétrages par des
monter: 2.1 Paramétrages
précédent: 2.1 Paramétrages
Table des matières
![]() est le complémentaire du pôle nord
est le complémentaire du pôle nord ![]() de la sphère
de la sphère
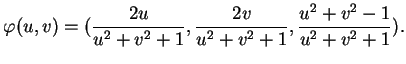
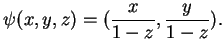
.