2.1.3 Equivalence

Si on compose un paramétrage $\varphi:U\to V$ avec une bijection $\theta:U'\to U$, où $U'$ est un ouvert de ${\rm I\!R}^p$, on obtient encore un paramétrage $\varphi\circ\theta$, du même ensemble $V$, pour autant que $\theta_{*}$ soit partout non singulier dans $U'$ (^2.2). On dit que les paramétrages $\varphi\circ\theta$ et $\varphi$ sont équivalents. Nous acceptons la propriété suivante sans démonstration.

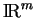
Théorème 7   Soit une partie $V$ de ${\rm I\!R}^m$ admettant un paramétrage $\varphi:U\subset {\rm I\!R}^p\to V$.
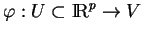
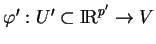
a)Tout paramétrage $\varphi': U'\subset{\rm I\!R}^{p'}\to V$ est équivalent à $\varphi$. En particulier, $p'=p$.
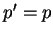
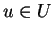
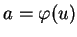
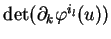
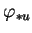
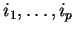
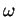
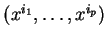
b)Soient $u\in U$ et $a=\varphi(u)$. Si le mineur $\det(\partial_k\varphi^{i_l}(u))$ de $\varphi_{*u}$ correspondant aux composantes d'indices $i_1,\ldots,i_p$ de $\varphi$ n'est pas nul, alors il existe un ouvert $\omega$ de $V$ contenant $a$ et admettant un paramétrage par les coordonnées $(x^{i_1},\ldots,x^{i_p})$.