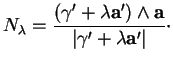
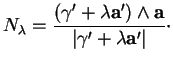
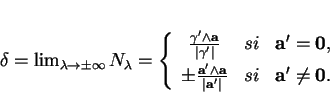
(i)Si
![]() ,
,
![]() est orthogonal à
est orthogonal à ![]() et est tangent à
et est tangent à ![]() en chaque point de
en chaque point de
![]() (5.16).
(5.16).
(ii)Si
![]() , il existe un seul
, il existe un seul ![]() pour lequel
pour lequel
![]() est parallèle à
est parallèle à ![]() .
.
Le point
Si
![]() , alors on dit que la génératrice
, alors on dit que la génératrice
![]() est cylindrique.
est cylindrique.
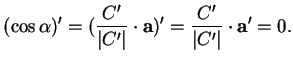
En raison de cette propriété, lorsque la ligne de striction est une droite, on dit que ![]() est un conoïde.
est un conoïde.