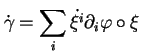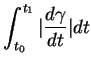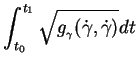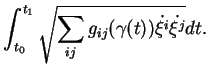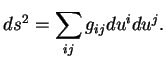suivant: 6.1.4 Distances & géodésiques
monter: 6.1 La première forme
précédent: 6.1.2 Equations de structure
Table des matières
Soit une courbe
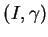 tracée sur
tracée sur  et contenue dans l'ouvert paramétré par
et contenue dans l'ouvert paramétré par
 . Il existe une courbe
. Il existe une courbe
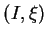 de
de 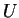 telle que
telle que
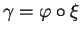 . C'est évident si
. C'est évident si
 est un paramétrage par des coordonnées et cela reste vrai
pour un paramétrage
quelconque qui est toujours localement équivalent à un paramétrage
par des coordonnées. Le vecteur tangent à
est un paramétrage par des coordonnées et cela reste vrai
pour un paramétrage
quelconque qui est toujours localement équivalent à un paramétrage
par des coordonnées. Le vecteur tangent à 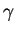 s'écrit donc
s'écrit donc
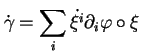 |
(6.1) |
(en désignant par un point la dérivée par rapport à 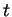 ).
Par conséquent, la longueur de l'arc de
).
Par conséquent, la longueur de l'arc de 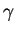 compris entre
compris entre
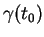 et
et
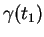 est, en calculant l'abscisse
curviligne
est, en calculant l'abscisse
curviligne 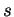 à partir d'une origine
quelconque et dans l'orientation associée au paramétrage
à partir d'une origine
quelconque et dans l'orientation associée au paramétrage 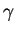 ,
,
Cette formule est souvent présentée sous la forme (6.3)




suivant: 6.1.4 Distances & géodésiques
monter: 6.1 La première forme
précédent: 6.1.2 Equations de structure
Table des matières