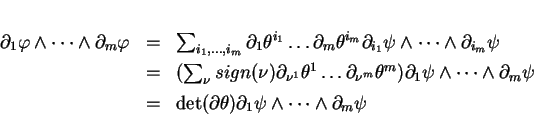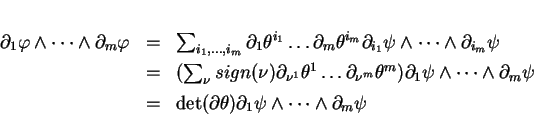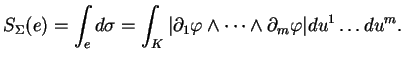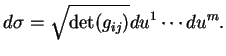suivant: 6.1.7 Un théorème d'Archimède
monter: 6.1.6 Mesure des aires
précédent: 6.1.6.2 Produit vectoriel
Table des matières
La norme
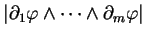 du produit
vectoriel des
du produit
vectoriel des
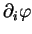 est un bon candidat
pour jouer le rôle "d'élément de surface" sur
est un bon candidat
pour jouer le rôle "d'élément de surface" sur  (6.10). Il généralise
en effet à la dimension quelconque
(6.10). Il généralise
en effet à la dimension quelconque 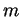 les définitions adoptées en
dimensions
les définitions adoptées en
dimensions  et
et 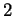 . De
plus, il mesure le volume (m-dimensionnel) du paralléllépipède
construit sur les
. De
plus, il mesure le volume (m-dimensionnel) du paralléllépipède
construit sur les
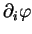 et, dans
et, dans
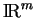 , l'unité de
mesure est précisément la mesure
du paralléllépidpède construit sur les vecteurs de la base canonique.
Un argument supplémentaire vient du comportement de cette norme sous
l'action d'un changement
de paramétrage. Si
, l'unité de
mesure est précisément la mesure
du paralléllépidpède construit sur les vecteurs de la base canonique.
Un argument supplémentaire vient du comportement de cette norme sous
l'action d'un changement
de paramétrage. Si 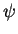 est un paramétrage de
est un paramétrage de  au voisinage
de
au voisinage
de  , il est équivalent à
, il est équivalent à  au voisinage de
au voisinage de  :
:
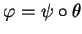 , où
, où
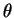 est un changement de variables. On a
la dernière somme portant sur les permutations
est un changement de variables. On a
la dernière somme portant sur les permutations 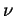 de
de
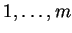 .
Ainsi
Ceci montre que
.
Ainsi
Ceci montre que
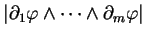 se comporte
comme un intégrand sous l'action d'un changement de variables
régulier entre
ouverts de
se comporte
comme un intégrand sous l'action d'un changement de variables
régulier entre
ouverts de
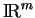 . Nous appellerons donc
l'élément de surface de
. Nous appellerons donc
l'élément de surface de  , la mesure ou la surface
d'une partie
, la mesure ou la surface
d'une partie
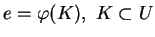 , de
, de  étant alors
étant alors
L'élément de surface s'exprime au moyen de la première forme
fondamentale.
C'est immédiat compte tenu de la Proposition
45.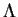




suivant: 6.1.7 Un théorème d'Archimède
monter: 6.1.6 Mesure des aires
précédent: 6.1.6.2 Produit vectoriel
Table des matières