6.1.1 Définition

On note $\Sigma$ une hypersurface de dimension $m$ (elle est donc plongée dans ${\rm I\!R}^{m+1}$), $(U,\varphi)$ un paramétrage d'un ouvert de $\Sigma$ et $(\Omega,F)$ une équation cartésienne de $\Sigma$ décrivant cet ouvert. Nous supposons $\Sigma$ de classe $C^k$, avec $k\geq 2$.

Par définition, la première forme fondamentale de $\Sigma$ en $a$ est la restriction $g_a$ du produit scalaire de ${\rm I\!R}^{m+1}$ à $\overrightarrow{T_a\Sigma}$:

$$g_a:h,k\in\overrightarrow{T_a\Sigma}\mapsto g_a(h,k)=h.k\in{\rm I\!R}.$$

On peut l'exprimer à l'aide du paramétrage $(U,\varphi)$ en décomposant les éléments de $\overrightarrow{T_a\Sigma}$ dans la base $(\partial_1\varphi,\ldots,\partial_m\varphi)$(^6.1). Si les composantes de $h$ et de $k$ selon celle-ci sont respectivement $(\lambda^1,\ldots,\lambda^m)$ et $(\mu^1,\ldots,\mu^m)$, alors

$$g_a(h,k)=\sum_{ij}\lambda^i\mu^j\partial_i\varphi.\partial_j\varphi=\sum g_{ij}(a)\lambda^i\mu^j$$

où on a posé $g_{ij}(a)=\partial_i\varphi.\partial_j\varphi$.

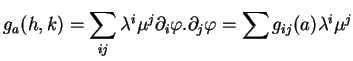
On peut se demander jusqu'à quel point le choix d'un paramétrage convenable permet de simplifier les coefficients $g_{ij}$ de la première forme fondamentale. En particulier, existe-t-il un paramétrage dans lequel ils sont constants? En général, un tel paramétrage n'existe pas et la détermination des formes locales canoniques que l'on peut donner à la première forme fondamentale est une question difficile qui ne sera pas étudiée ici. Nous nous contenterons d'énoncer un théorème important, valable pour les surfaces plongées dans ${\rm I\!R}^3$ et que nous accepterons sans démonstration.

Théorème 36   Soit une surface $V$ plongée dans ${\rm I\!R}^3$. Tout point $a\in V$ admet un voisinage qui est l'image d'un paramétrage dans lequel $g_{11}=g_{22}$ et $g_{12}=g_{21}=0$.

Les paramétrages ayant cette propriété conservent les angles(^6.2) et, pour cette raison, ils sont dits conformes.