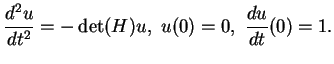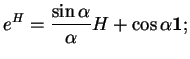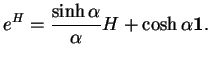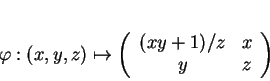
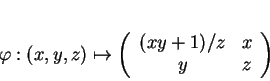
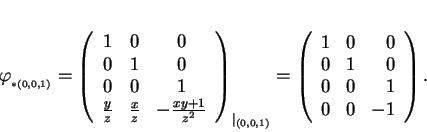
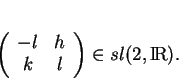
La fonction ![]() est donnée par(5.8)
est donnée par(5.8)
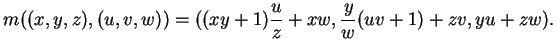
L'application
![]() s'obtient en bloquant le premier argument
de
s'obtient en bloquant le premier argument
de ![]() à la valeur
à la valeur ![]() . On a donc
. On a donc
![\begin{displaymath}
% latex2html id marker 19017
\left (
\begin{array}{ccc}
\fra...
...\frac{y}{w^2}\\ [1ex]
y&0& z
\end{array}\right )_{\vert(0,0,1)}\end{displaymath}](img921.gif) |
|||
![\begin{displaymath}
% latex2html id marker 19021
\left (
\begin{array}{ccc}
\frac{xy+1}{z}&0&x\\ [1ex]
0&z&-y\\ [1ex]
y&0& z
\end{array}\right )
.\end{displaymath}](img922.gif) |
![\begin{displaymath}
% latex2html id marker 19023\left\{
\begin{array}{cclc}
{\...
...\ [1ex]
{\frac{d{z}}{dt}}&=&hy+lz&,z(0)=1.
\end{array}\right.
\end{displaymath}](img923.gif)
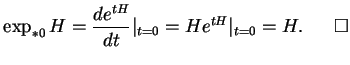
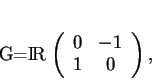
Voyons à quoi ressemble le paramétrage par l'exponentielle dans le
cas de
![]() . Cherchons
. Cherchons
![]() lorsque
lorsque
![]() sous la
forme(5.9)
sous la
forme(5.9)
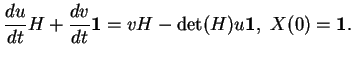
![\begin{displaymath}
% latex2html id marker 19093\left\{
\begin{array}{ll}
{\fr...
... [1ex]
{\frac{d{v}}{dt}}=-\det(H)u&,v(0)=1.
\end{array}\right.
\end{displaymath}](img941.gif)