


suivant: 5.3.2.2 Le quotient de
monter: 5.3.2 Fonctions homogènes
précédent: 5.3.2 Fonctions homogènes
Table des matières
Considérons par exemple la fonction
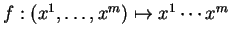 , homogène de poids
, homogène de poids
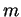 . Si
. Si 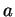 est un point stationnaire de
est un point stationnaire de 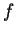 sur
sur 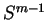 , il existe
, il existe
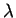 tel que
(l'accent circonflexe indique l'omission.) Il est facile de vérifier
que les points stationnaires dont aucune composante n'est nulle (les
autres sont sans
importance en l'occurrence car
tel que
(l'accent circonflexe indique l'omission.) Il est facile de vérifier
que les points stationnaires dont aucune composante n'est nulle (les
autres sont sans
importance en l'occurrence car 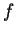 s'y annule) sont les points
où les signes sont choisis arbitrairement pour chaque composante. Le
minimum et le maximum absolus de
s'y annule) sont les points
où les signes sont choisis arbitrairement pour chaque composante. Le
minimum et le maximum absolus de 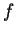 sont donc
sont donc
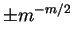 .
Ainsi,
Les
.
Ainsi,
Les 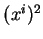 représentant des nombres non négatifs
représentant des nombres non négatifs 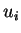 arbitraires, il vient en élevant au carré et en extrayant la racine
m-ième
En pistant les calculs, on voit en outre que l'égalité est réalisée
si et seulement si les
arbitraires, il vient en élevant au carré et en extrayant la racine
m-ième
En pistant les calculs, on voit en outre que l'égalité est réalisée
si et seulement si les 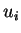 sont égaux (5.13).
sont égaux (5.13).
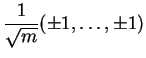
![$\displaystyle \sqrt[m]{u_1\cdots u_m}\leq \frac{u_1+\cdots +u_m}{m}.
$](img1049.gif)