5.1 Espace tangent

Un vecteur tangent à une partie $V\subset{\rm I\!R}^m$ en $a\in V$ est un vecteur de la forme ${\frac{d{\gamma}}{dt}}_{\vert t=s}$ où $\gamma$ est une application de classe $C^k$ d'un intervalle ouvert $I$ de ${\rm I\!R}$ dans ${\rm I\!R}^m$ telle que $\gamma(I)\subset V$ et telle que $\gamma(s)=a$(^5.1).

L'ensemble des vecteurs tangent à $V$ en $a$ est noté $\overrightarrow{T_aV}$. L'espace tangent à $V$ en $a$ est l'ensemble $a+\overrightarrow{T_aV}$.

Proposition 23   Soient une variété plongée $V\subset{\rm I\!R}^m$, un paramétrage $(U,\varphi)$, $u\in U$ et une équation cartésienne $(\Omega,F)$ d'un voisinage ouvert de $a=\varphi(u)$ dans $V$. On a

$$\overrightarrow{T_aV}={\rm im}\varphi_{*u}=\ker F_{*a}.$$

En particulier, $T_aV$ est une sous-variété affine de ${\rm I\!R}^m$, de dimension $p=\dim_aV$.

Soit $v\in{\rm I\!R}^p$. Pour $t$ assez petit, $u+tv\in U$ et $t\mapsto \varphi(u+tv)$ est une courbe définie au voisinage de 0, tracée sur $V$ et passant par $a$ en $t=0$. Par conséquent $\varphi_{*u}v\in \overrightarrow{T_aV}$. Soit alors $h={\frac{d{\gamma}}{dt}}_{\vert t=s}\in \overrightarrow{T_aV}$, où $\gamma$ est une courbe de $V$ passant par $a$ en $t=s$. Pour $t$ assez voisin de $s$, $\gamma(t)\in\Omega$. De là, $F\circ\gamma(t)=0$ dans un voisinage de $s$. En dérivant cette relation par rapport à $t$ en $t=s$, il vient $F_{*a}h=0$. Au total

$${\rm im}\varphi_{*u}\subset \overrightarrow{T_aV}\subset\ker F_{*a}.$$

Les deux membres extrêmes de ces inclusions sont des sous-espaces vectoriels de dimensions $p$ de ${\rm I\!R}^m$. Il sont donc égaux.$\qedsymbol$

Le paramétrage $(U,\varphi)$ fournit donc une base de $\overrightarrow{T_aV}$, à savoir

$$(\partial_1\varphi(u),\ldots,\partial_p\varphi(u))$$

où $u=\varphi^{-1}(a)$. L'équation cartésienne $(\Omega,F)$ donne quant à elle une base du complément orthogonal $\overrightarrow{T_aV}^\perp$ du sous vectoriel directeur de $T_aV$,

$$({\rm grad}_a F^1,\ldots,{\rm grad}_a F^{m-p})$$

La variété affine $a+\overrightarrow{T_aV}^\perp$ s'appelle espace normal à $V$ en $a$.

Pour une hypersurface, l'hyperplan tangent en $a$ admet ainsi l'équation cartésienne

$$\sum_i(x^i-a^i)\partial_iF(a)=0.$$

Par exemple, l'espace tangent en $a$ à une quadrique $Q$ d'équation cartésienne $Ax.x+2b.x+c=0$ admet l'équation $(Aa+b).(x-a)=0$, qui s'écrit aussi

$$Aa.x+b.(a+x)+c=0 \ (\footnotemark ).$$

Sous cette forme, on l'appelle équation au dédoublement car on l'optient à partir de l'équation de la quadrique en y remplaçant $x^ix^j$ par $(a^ix^j+x^ia^j)/2$, et $x^i$ par $(a^i+x^i)/2$. Les tangentes aux coniques d'équations $\alpha x^2+\beta y^2=1$ et $y^2=\gamma x$ en le point de composantes $(u,v)$ admettent ainsi respectivement les équations $\alpha ux+\beta vy=1$ et $2vy=\gamma(u+x)$.

Proposition 24   Si une variété plongée $V$ contient une droite ${\mathcal D}$ alors le plan tangent à $V$ en chaque point $a\in{\mathcal D}$ contient ${\mathcal D}$.

La droite est l'image d'une courbe tracée sur $V$. Les vecteurs directeurs de ${\mathcal D}$ sont donc tangents à $V$ en chaque point ${\mathcal D}$. Par conséquent, si $a\in{\mathcal D}$, alors ${\mathcal D}\subset T_aV$ car ${\mathcal D}$ est parallèle à l'hyperplan $T_aV$ et le rencontre en $a$.$\qedsymbol$

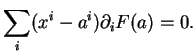
Par chaque point d'un hyperboloïde à une nappe, il passe deux droites contenues dans cet hyperboloïde. Il en va de même pour un paraboloïde hyperbolique. L'un et l'autre sont donc des unions de droites à l'instar des cônes et des cylindres mais ces droites ne passent pas un point fixe et ne sont pas parallèles à une même direction.

C'est un exercice intéressant que de vérifier l'existence de ces droites.