6.1.4 Distances & géodésiques

Les variétés plongées possèdent une famille de courbes distinguées, les géodésiques, qui sont aux variétés courbes ce que les droites sont aux espaces euclidiens. Pour définir celles-ci dans le cas d'une hypersurface, nous allons adopter un point de vue "mécaniste", la mécanique à laquelle nous nous référons étant la mécanique classique. D'après le principe d'inertie, un point matériel qui n'est soumis à aucune force est animé d'un mouvement rectiligne et uniforme. Selon la seconde loi de Newton, l'accélération est proportionnelle à la résultante des forces qui s'exercent sur le point matériel, son accélération est alors nulle. Si ce point est astreint à se déplacer sur une surface, cela revient à supposer que cette accélération est normale à celle-ci en tout point. En effet, d'après le principe d'action/réaction, la force qui pourrait résulter de cette composante de l'accélération est neurtalisée par une réaction opposée maintenant le point sur la surface. Forts de cette image, nous appelons géodésique de $\Sigma$ toute courbe $(I,\gamma)$ tracée sur $\Sigma$ dont "l'accélération" $\ddot{\gamma}$ est constamment normale à $\Sigma$:

$$\ddot{\gamma}(t)\perp T_{\gamma(t)}\Sigma,\ \forall t\in I.$$

Dans la proposition suivante, les notations sont celles adoptées au paragraphe précédent.

Proposition 38   Une courbe $(I,\gamma=\varphi\circ\xi)$ de $\Sigma$ est une géodésique si et seulement si $\xi$ est une solution du système d' équations différentielles

$$\ddot{\xi}^k+\sum_{ij}(\Gamma^k_{ij}\circ\xi)\dot{\xi^i}\dot{\xi}^j=0,\ k=1,\ldots,n.$$

Dérivons la relation (12). Il vient

$$\ddot{\gamma}=\sum_{ij}\partial_{ij}(\varphi\circ\xi)\dot{\xi}^i\dot{\xi}^j+\sum_k(\partial_k\varphi\circ\xi)\ddot{\xi}^k.$$ (6.2)

D'après les équations de structures, la composante parallèle à $T_\gamma\Sigma$ de cette expression est

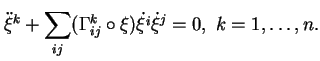
$$\sum_k[\ddot{\xi}^k+\sum_{ij}(\Gamma^k_{ij}\circ\xi)\dot{\xi^i}\dot{\xi}^j]\partial_k\varphi\circ\xi.$$

D'où la proposition.$\qedsymbol$

En posant $\eta^i=\dot{\xi^i}$, on transforme le système d'équations ci-dessus en un système du premier ordre en les fonctions $\xi^i$ et $\eta^i$. Une solution de ces équations est déterminée par ses conditions initiales. Cela revient à imposer les valeurs de $\gamma(t)$ et de $\dot{\gamma}(t)$ en un point $t=t_0$. On peut alors établir la proposition suivante, dont nous ne détaillerons pas la démonstration.

Corollaire 39   Soient $a\in\Sigma$ et $h\in\overrightarrow{T_a\Sigma}$. Il existe une seule (^6.4) géodésique $\gamma$ telle que $\gamma(0)=a$ et $\dot{\gamma}(0)=h$.

Proposition 40   Si $(I,\gamma)$ est une géodésique de $\Sigma$, alors $\vert\dot{\gamma}\vert$ est constant.

En effet, la dérivée de $\vert\dot{\gamma}\vert^2$ est $2\dot{\gamma}.\ddot{\gamma}$. Elle est donc nulle puisque $\ddot{\gamma}$ est normal à $\Sigma$ en $\gamma$ et $\dot{\gamma}$ lui est tangent en ce point.$\qedsymbol$

Le "mouvement" le long d'une géodésique est donc "uniforme" puisque sa vitesse est d'intensité constante. De plus, cette propriété signifie que le paramètre $t$ dont dépend une géodésique est un multiple constant de l'abscisse curviligne. Dailleurs, il est clair que, $r$ étant un nombre non nul, $\gamma(t)$ est une géodésique si et seulement si $\gamma(rt)$ en est une.

Sur un cylindre circulaire droit, les géodésiques dessinent des hélices circulaires. Cela résulte du fait que dans le paramétrage rappelé plus haut, les symboles de Christoffel sont nuls. En particulier les génératrices et les cercles contenus dans les plans perpendiculaires aux génératrices sont des géodésiques. En déroulant le cylindre sur un de ses plans tangents, on voit que ses géodésiques tracent des droites du plan. On aurait pu, inversement, déterminer les géodésiques du cylindre en utilisant le fait qu'il est développable.

Sur une sphère de ${\rm I\!R}^3$, ce sont les arcs de grand cercle, rapportés aux multiples constants de l'abscisse curviligne, qui sont les géodésiques. En effet, "l'accélération" de toute courbe $(I,\gamma)$ se décompose en ses parties tangentielle et normale

$$\ddot{\gamma}=\dot{v}{\bf t}+v^2\kappa{\bf n}$$

où $v=\vert\dot{\gamma}\vert$, $\kappa$ est la courbure de $\gamma$ et ${\bf t},{\bf n}$ sont sa tangente unitaire et sa normale principale respectivement. Par conséquent, si $v$ est constant, $\ddot{\gamma}$ est parallèle à ${\bf n}$. Or il se fait que la normale principale à un grand cercle est toujours normale à la sphère puisqu'il est contenu dans un plan diamétral. Par conséquent, les grand cercles sont des géodésiques pourvu qu'ils soient paramétrés par un multiple de l'abscisse curviligne. Comme par un point, il passe toujours un grand cercle tangent à une direction quelconque de la sphère en ce point, il n'y a pas d'autres géodésiques.

Revenons au cas général. On peut montrer que s'ils sont assez voisins, deux points $x, y$ de $\Sigma$ sont les extrémités d'un seul arc de géodésique dont la longueur est la plus petite des longueurs des arcs qu'ils délimitent sur des courbes tracées sur $\Sigma$. On définit alors la distance séparant $x$ et $y$ comme étant la longueur de cet arc de géodésique.

La première forme fondamentale d'une variété $V$ plongée dans ${\rm I\!R}^m$ est définie comme dans le cas des hypersurfaces: en chaque point, c'est aussi la restriction du produit scalaire de ${\rm I\!R}^m$au sous-vectoriel directeur de l'espace tangent à $V$ en ce point. La longueur d'un arc de courbe de $V$ est semblablement donnée par la même formule que pour un arc de courbe d'une hypersurface. Pour tous points $x,y\in V$, on note alors $d_V(x,y)$ la meilleure borne inférieure des longueurs des arcs que ces points délimitent sur des courbes tracées sur $V$. On peut montrer que

$$d_V: (x,y)\in V\times V\mapsto d_V(x,y)\in {\rm I\!R}$$

est une distance sur $V$ et que la topologie d'espace métrique(^6.5) de $(V,d_V)$ est la topologie induite par ${\rm I\!R}^m$ sur $V$.