


suivant: 7.2 Quelques propriétés des
monter: 7 Inégalité isopérimétrique
précédent: 7 Inégalité isopérimétrique
Table des matières
Peut-on déterminer la surface maximale correspondant à un périmètre donné?
La notion de surface d'un ensemble
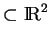 ne pose pas de problème. C'est, si elle existe, la mesure de Lebesgues de
ne pose pas de problème. C'est, si elle existe, la mesure de Lebesgues de 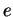 . La notion de périmètre, par contre, n'est pas simple à définir.
Pour un polygone convexe, il s'agit de la somme des longueurs des côtés. Lorsque
. La notion de périmètre, par contre, n'est pas simple à définir.
Pour un polygone convexe, il s'agit de la somme des longueurs des côtés. Lorsque 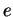 est délimité par un arc régulier de courbe, la notion est également bien définie. On peut étendre ces deux cas particuliers aux ensembles convexes compacts (non vides) en dimension quelconque. On parle alors de volume et de surface latérale et on peut établir que pour une surface latérale donnée, c'est le volume de la sphère qui est le plus grand.
est délimité par un arc régulier de courbe, la notion est également bien définie. On peut étendre ces deux cas particuliers aux ensembles convexes compacts (non vides) en dimension quelconque. On parle alors de volume et de surface latérale et on peut établir que pour une surface latérale donnée, c'est le volume de la sphère qui est le plus grand.
Nous allons vérifier cela dans l'ensemble des convexes compacts d'intérieur non vide dont la frontière est une variété plongée dans
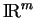 . La stratégie de la démonstration repose sur deux faits. Le premier est l'inégalité de Brunn-Minkowski:
. La stratégie de la démonstration repose sur deux faits. Le premier est l'inégalité de Brunn-Minkowski:
Le second s'énonce comme suit, en notant 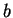 la boule (7.1) de centre 0 et de rayon
la boule (7.1) de centre 0 et de rayon 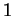 :
:
Proposition 56
Pour tout convexe compact
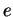
de
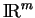
, d'intérieur non vide, il existe
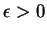
tel que
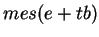
soit un polynôme homogène de degré
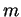
dans
![$ [0,\epsilon]$](img1541.gif)
(
7.2). De plus, si
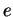
est un polytope ou si sa frontière est une hypersurface de
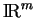
, alors le coefficient de
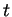
dans de polynôme est la surface latérale de
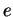
.
En vertu de cette proposition, il est légitime d'appeler surface latérale de 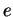 le coefficient de
le coefficient de 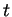 dans le polynôme
dans le polynôme 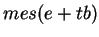 . Ceci est d'ailleurs assez intuitif. En effet, ce coefficient vaut
. Ceci est d'ailleurs assez intuitif. En effet, ce coefficient vaut
et on imagine volontiers que, lorsque 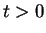 est très petit, la mesure de la ``gangue''
est très petit, la mesure de la ``gangue''
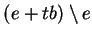 soit fort proche du produit de
soit fort proche du produit de 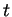 et de la mesure de la surface latérale de
et de la mesure de la surface latérale de 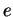 .
En particulier, puisque
on voit que la surface latérale de la boule
.
En particulier, puisque
on voit que la surface latérale de la boule 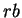 de rayon
de rayon 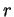 dans
dans
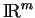 est la dérivée
est la dérivée
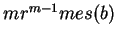 par rapport à
par rapport à 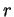 de son volume
de son volume
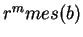 .
.
Cela étant, il vient
Proposition 57
Si
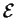
est un ensemble de parties
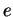
de

pour lesquelles
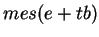
est un polynôme
en
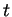
pour
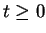
voisin de 0, alors pour tout
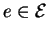
,
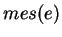
est au plus égal
au volume de la boule dont la surface latérale est égale à
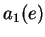
.
Appliquons l'inégalité de Brunn-Minkowski avec 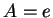 et
et 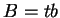 , en notant que, pour
, en notant que, pour 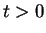 ,
,
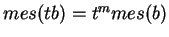 . En élevant les deux membres à la puissance
. En élevant les deux membres à la puissance 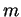 , on obtient d'abord
où
, on obtient d'abord
où 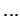 désigne des polynômes divisibles par
désigne des polynômes divisibles par 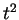 .
En simplifiant par
.
En simplifiant par 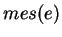 , puis par
, puis par 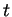 et en laissant enfin tendre
et en laissant enfin tendre 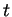 vers 0, on obtient l'inégalité
Il en résulte aussitôt que si
vers 0, on obtient l'inégalité
Il en résulte aussitôt que si 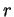 est choisi pour que la surface latérale de
est choisi pour que la surface latérale de 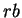 soit
soit 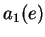 , c'est-à-dire pour que
, c'est-à-dire pour que
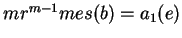 , alors
, alors
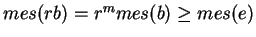 .
.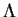
Nous démontrerons l'inégalité de Brunn-Minkowski. Nous allons vérifier la Proposition 56 lorsque 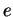 est un polygone convexe et nous l'établirons lorsqu'il est un convexe compact d'intérieur non vide dont la frontière est une hypersurface.
est un polygone convexe et nous l'établirons lorsqu'il est un convexe compact d'intérieur non vide dont la frontière est une hypersurface.
Si 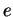 est un polygone convexe, alors
est un polygone convexe, alors 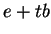 est l'union
est l'union
- de
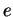
- des rectangles de largeur
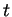 et dont les longueurs sont les différents côtés de
et dont les longueurs sont les différents côtés de 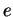
- des secteurs de cercle de rayon
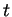 centrés en chaque sommet de
centrés en chaque sommet de 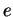 et délimités par les perpendiculaires aux côtés issus du sommet
et délimités par les perpendiculaires aux côtés issus du sommet
Par conséquent, la somme des angles formés par ces perpendiculaires valant 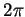 , pour un polygone convexe
, pour un polygone convexe 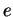 ,
,
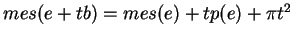 , où
, où 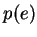 est le périmètre de
est le périmètre de 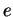 .
.
Pour un polyèdre compact dans un espace de dimension 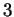 , le développement est analogue. Le coefficient du terme en
, le développement est analogue. Le coefficient du terme en 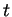 est la somme des surfaces des faces du polyèdre; celui de
est la somme des surfaces des faces du polyèdre; celui de 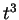 est le volume de la boule
est le volume de la boule 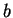 . Il y a un coefficient supplémentaire, celui de
. Il y a un coefficient supplémentaire, celui de 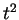 , qui comptabilise les contributions des arêtes de
, qui comptabilise les contributions des arêtes de 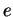 . Chaque arête correspond dans
. Chaque arête correspond dans 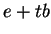 à une portion de cylindre circulaire droit dont la hauteur est l'arête considérée et dont la mesure dépend de l'angle que forment les deux faces de
à une portion de cylindre circulaire droit dont la hauteur est l'arête considérée et dont la mesure dépend de l'angle que forment les deux faces de 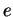 qui aboutissent en cette arête. Ces angles ne sont en général pas tous égaux et il n'y a pas d'expression simple de ce coefficient faisant par exemple intevenir le ``périmètre'' de
qui aboutissent en cette arête. Ces angles ne sont en général pas tous égaux et il n'y a pas d'expression simple de ce coefficient faisant par exemple intevenir le ``périmètre'' de 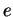 .
.
Les angles en question sont aux polyèdres ce que la courbure est aux surface. Nous établirons en effet que si la frontière de 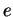 est une hypersurface, les coefficients des termes de degré supérieur à
est une hypersurface, les coefficients des termes de degré supérieur à 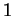 de
de 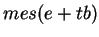 s'expriment à l'aide de des courbures principales de celle-ci.
s'expriment à l'aide de des courbures principales de celle-ci.



suivant: 7.2 Quelques propriétés des
monter: 7 Inégalité isopérimétrique
précédent: 7 Inégalité isopérimétrique
Table des matières
![]() . La stratégie de la démonstration repose sur deux faits. Le premier est l'inégalité de Brunn-Minkowski:
. La stratégie de la démonstration repose sur deux faits. Le premier est l'inégalité de Brunn-Minkowski:
![]() le coefficient de
le coefficient de ![]() dans le polynôme
dans le polynôme ![]() . Ceci est d'ailleurs assez intuitif. En effet, ce coefficient vaut
. Ceci est d'ailleurs assez intuitif. En effet, ce coefficient vaut
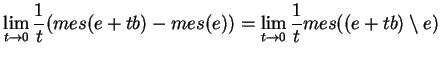
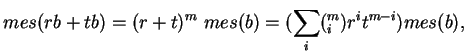
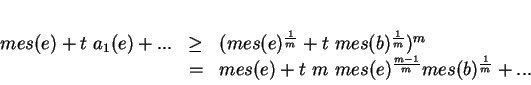
![]() est un polygone convexe et nous l'établirons lorsqu'il est un convexe compact d'intérieur non vide dont la frontière est une hypersurface.
est un polygone convexe et nous l'établirons lorsqu'il est un convexe compact d'intérieur non vide dont la frontière est une hypersurface.
![]() est un polygone convexe, alors
est un polygone convexe, alors ![]() est l'union
est l'union
![]() , le développement est analogue. Le coefficient du terme en
, le développement est analogue. Le coefficient du terme en ![]() est la somme des surfaces des faces du polyèdre; celui de
est la somme des surfaces des faces du polyèdre; celui de ![]() est le volume de la boule
est le volume de la boule ![]() . Il y a un coefficient supplémentaire, celui de
. Il y a un coefficient supplémentaire, celui de ![]() , qui comptabilise les contributions des arêtes de
, qui comptabilise les contributions des arêtes de ![]() . Chaque arête correspond dans
. Chaque arête correspond dans ![]() à une portion de cylindre circulaire droit dont la hauteur est l'arête considérée et dont la mesure dépend de l'angle que forment les deux faces de
à une portion de cylindre circulaire droit dont la hauteur est l'arête considérée et dont la mesure dépend de l'angle que forment les deux faces de ![]() qui aboutissent en cette arête. Ces angles ne sont en général pas tous égaux et il n'y a pas d'expression simple de ce coefficient faisant par exemple intevenir le ``périmètre'' de
qui aboutissent en cette arête. Ces angles ne sont en général pas tous égaux et il n'y a pas d'expression simple de ce coefficient faisant par exemple intevenir le ``périmètre'' de ![]() .
.
![]() est une hypersurface, les coefficients des termes de degré supérieur à
est une hypersurface, les coefficients des termes de degré supérieur à ![]() de
de ![]() s'expriment à l'aide de des courbures principales de celle-ci.
s'expriment à l'aide de des courbures principales de celle-ci.