



suivant: 7.2.3 Convexes d'intérieur non
monter: 7.2 Quelques propriétés des
précédent: 7.2.1 Distance d'un point
Table des matières
On dit qu'un hyperplan est un hyperplan d'appui d'un convexe  si
si  rencontre cet hyperplan et s'il est contenu dans un des demi-espaces que celui-ci délimite. Les hyperplans d'appui sont un peu aux convexes ce que les espaces tangents sont aux variétés plongées.
rencontre cet hyperplan et s'il est contenu dans un des demi-espaces que celui-ci délimite. Les hyperplans d'appui sont un peu aux convexes ce que les espaces tangents sont aux variétés plongées.
Il se pourrait que  soit tout entier contenu dans un de ses hyperplans d'appui
soit tout entier contenu dans un de ses hyperplans d'appui 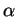 . Si ce n'est pas le cas (7.3) alors on peut distinguer sans ambiguité les normales unitaires à
. Si ce n'est pas le cas (7.3) alors on peut distinguer sans ambiguité les normales unitaires à 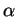 . Une pointe vers le demi-espace contenant
. Une pointe vers le demi-espace contenant  . Nous l'appellerons la normale orientée vers l'intérieur. L'autre est la normale orientée vers l'extérieur, elle pointe vers le demi-espace ne contenant pas
. Nous l'appellerons la normale orientée vers l'intérieur. L'autre est la normale orientée vers l'extérieur, elle pointe vers le demi-espace ne contenant pas  .
.
Nous notons encore  un convexe fermé.
un convexe fermé.
Proposition 60
Par tout point de la frontière de

, il passe un hyperplan d'appui de

.
Soit un point frontière  de
de  . Il est limite d'une suite de points
. Il est limite d'une suite de points 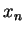 n'appartenant pas à
n'appartenant pas à  . Quitte à passer à une sous-suite, on peut supposer que la suite
. Quitte à passer à une sous-suite, on peut supposer que la suite
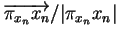 tend vers une limite
tend vers une limite 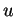 . Vu la continuité de l'application
. Vu la continuité de l'application
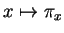 ,
, 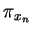 tend vers
tend vers 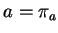 . Il est alors clair que l'hyperplan perpendiculaire à
. Il est alors clair que l'hyperplan perpendiculaire à 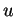 et passant par
et passant par  est un hyperplan d'appui de
est un hyperplan d'appui de  .
.
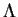
Il n'y a pas nécessairement qu'un seul hyperplan d'appui passant par un point frontière donné. Par exemple, toutes les droites passant par un sommet d'un polygone balayant l'angle extérieur délimité par les deux côtés issus de ce sommet sont des droites d'appui du poygone. De même, tous les plans qui contiennent une tangente au cercle qui délimite un disque dans
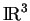 sont des plans d'appui du disque.
sont des plans d'appui du disque.
Proposition 61
Si la frontière de

est une variété plongée, alors les hyperplans d'appui qui passent par
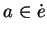
contiennent
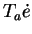
.
Soit 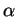 un hyperpan d'appui en
un hyperpan d'appui en  et un vecteur tangent
et un vecteur tangent 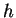 à
à 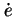 en
en  . Notons
. Notons 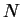 la normale de
la normale de 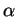 orientée vers l'extérieur (7.4) et considérons une courbe
orientée vers l'extérieur (7.4) et considérons une courbe 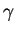 de
de 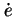 tangente à
tangente à 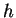 en
en 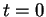 . Le point
. Le point  étant la projection de
étant la projection de 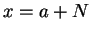 sur
sur  , la fonction
, la fonction
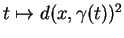 possède un minimum local en
possède un minimum local en 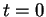 . Sa dérivée
. Sa dérivée
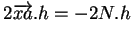 en
en 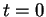 est donc nulle et
est donc nulle et 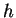 est parallèle à
est parallèle à 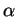 .
.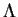




suivant: 7.2.3 Convexes d'intérieur non
monter: 7.2 Quelques propriétés des
précédent: 7.2.1 Distance d'un point
Table des matières
root
2007-12-09
![]() soit tout entier contenu dans un de ses hyperplans d'appui
soit tout entier contenu dans un de ses hyperplans d'appui ![]() . Si ce n'est pas le cas (7.3) alors on peut distinguer sans ambiguité les normales unitaires à
. Si ce n'est pas le cas (7.3) alors on peut distinguer sans ambiguité les normales unitaires à ![]() . Une pointe vers le demi-espace contenant
. Une pointe vers le demi-espace contenant ![]() . Nous l'appellerons la normale orientée vers l'intérieur. L'autre est la normale orientée vers l'extérieur, elle pointe vers le demi-espace ne contenant pas
. Nous l'appellerons la normale orientée vers l'intérieur. L'autre est la normale orientée vers l'extérieur, elle pointe vers le demi-espace ne contenant pas ![]() .
.
![]() un convexe fermé.
un convexe fermé.
![]() sont des plans d'appui du disque.
sont des plans d'appui du disque.