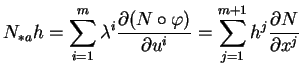suivant: 6.2.2 Equations de structure
monter: 6.2 La seconde forme
précédent: 6.2 La seconde forme
Table des matières
Pour compléter la description locale de
l'hypersurface  , il nous faut encore choisir une normale, au moins dans le
voisinage
, il nous faut encore choisir une normale, au moins dans le
voisinage
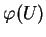 du point
du point  dans lequel nous l'étudions.
Dans la suite, nous supposerons disposer d'une fonction
dans lequel nous l'étudions.
Dans la suite, nous supposerons disposer d'une fonction 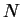 associant
de façon
continue à tout
associant
de façon
continue à tout
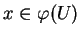 un élément
un élément
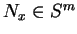 normal en
normal en
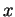 à
à  (6.12).
Il y a toujours deux choix possibles de vecteur normé perpendiculaire
à
(6.12).
Il y a toujours deux choix possibles de vecteur normé perpendiculaire
à
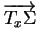 , opposés l'un à l'autre.
Par commoditié, nous supposerons que
, opposés l'un à l'autre.
Par commoditié, nous supposerons que 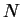 est donné par
lorsque nous l'exprimerons à l'aide du paramétrage
est donné par
lorsque nous l'exprimerons à l'aide du paramétrage  et nous
choisirons
lorsque nous aurons à le prolonger en une fonction dérivable dans un
voisinage de
et nous
choisirons
lorsque nous aurons à le prolonger en une fonction dérivable dans un
voisinage de  , ouvert dans
, ouvert dans
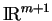 .
.
Par exemple, pour une quadrique sans point double 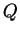 , d'équation
, d'équation
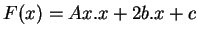 ,
,
tandis que pour
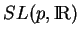 ,
,
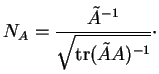 |
(6.6) |
Lorsqu'il est possible de définir 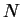 sur tout
sur tout  , on dit que
, on dit que
 est orientable.
L'application
est orientable.
L'application 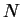 s'appelle alors l'application de Gauss de
s'appelle alors l'application de Gauss de
 .
.
En dérivant 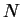 , nous pourrons nous faire une idée de la manière dont
il varie au voisinage d'un point, et donc appréhender la courbure de
, nous pourrons nous faire une idée de la manière dont
il varie au voisinage d'un point, et donc appréhender la courbure de
 .
Comme
.
Comme 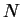 n'est défini que sur un ouvert de
n'est défini que sur un ouvert de  , il faut
préciser comment il est possible de le dériver.
, il faut
préciser comment il est possible de le dériver.
Soient
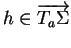 et une courbe
et une courbe
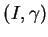 tracée sur
tracée sur
 , tangente à
, tangente à 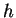 en
en 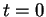 . Le lemme suivant montre que
. Le lemme suivant montre que
est bien défini, qu'il est linéaire en 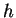 et indique comment le
calculer au moyen de
et indique comment le
calculer au moyen de  ou d'un prolongement de
ou d'un prolongement de 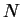 à un
voisinage de
à un
voisinage de  dans
dans
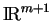 .
.
Notons
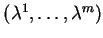 les composantes de
les composantes de
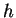 selon la base
selon la base
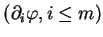 de
de
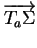 et
et
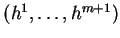 ses composantes dans la
base canonique de
ses composantes dans la
base canonique de
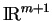 . Comme indiqué plus haut,
. Comme indiqué plus haut, 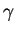 se factorise via
se factorise via
 : il existe une courbe
: il existe une courbe
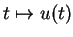 de
de 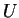 , définie au
voisinage de 0 et telle que
, définie au
voisinage de 0 et telle que
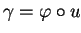 . On a alors
. On a alors
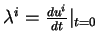 .
.
Lemme 48
On a
où, dans la seconde somme,
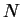
est supposé défini dans un voisinage
de

dans
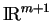
.
C'est, dans les deux cas, une application immédiate du théorème
de dérivation des fonctions composées.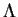




suivant: 6.2.2 Equations de structure
monter: 6.2 La seconde forme
précédent: 6.2 La seconde forme
Table des matières
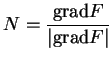
![]() , d'équation
, d'équation
![]() ,
,
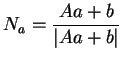
![]() , nous pourrons nous faire une idée de la manière dont
il varie au voisinage d'un point, et donc appréhender la courbure de
, nous pourrons nous faire une idée de la manière dont
il varie au voisinage d'un point, et donc appréhender la courbure de
![]() .
Comme
.
Comme ![]() n'est défini que sur un ouvert de
n'est défini que sur un ouvert de ![]() , il faut
préciser comment il est possible de le dériver.
, il faut
préciser comment il est possible de le dériver.
![]() et une courbe
et une courbe
![]() tracée sur
tracée sur
![]() , tangente à
, tangente à ![]() en
en ![]() . Le lemme suivant montre que
. Le lemme suivant montre que
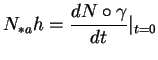
![]() les composantes de
les composantes de
![]() selon la base
selon la base
![]() de
de
![]() et
et
![]() ses composantes dans la
base canonique de
ses composantes dans la
base canonique de
![]() . Comme indiqué plus haut,
. Comme indiqué plus haut, ![]() se factorise via
se factorise via
![]() : il existe une courbe
: il existe une courbe
![]() de
de ![]() , définie au
voisinage de 0 et telle que
, définie au
voisinage de 0 et telle que
![]() . On a alors
. On a alors
![]() .
.