


suivant: 5.2.1.1 Illustration
monter: 5.2 Espace tangent aux
précédent: 5.2 Espace tangent aux
Table des matières
Rappelons que pour tout
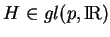 , l'équation différentielle
ordinaire
, l'équation différentielle
ordinaire
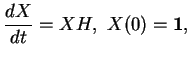 |
(5.1) |
admet une seule solution
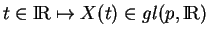 . Elle
est notée
. Elle
est notée 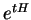 (5.3). La matrice
(5.3). La matrice 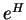 , parfois désignée par
, parfois désignée par 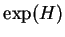 , s'appelle l'exponentielle de la matrice
, s'appelle l'exponentielle de la matrice 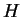 .
.
Proposition 26
Le groupe
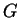
contient l'exponentielle de tous ses vecteurs tangents en
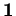
: si
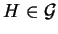
alors
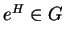
.
La démonstration est simple dans son idée. Elle est un peu délicate techniquement.
En voici le scénario. On fixe
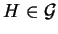 . Dans un premier temps, on montre que si
. Dans un premier temps, on montre que si
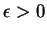 est assez petit, alors
est assez petit, alors
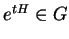 lorsque
lorsque
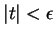 . Pour cela, on choisit un paramétrage
. Pour cela, on choisit un paramétrage
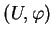 de
de 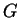 au voisinage de
au voisinage de 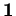 et on construit une solution de (7) sous la forme
et on construit une solution de (7) sous la forme
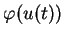 , où
, où
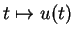 est une courbe de
est une courbe de 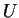 définie au voisinage de 0 et passant par
définie au voisinage de 0 et passant par
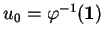 en
en 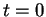 . A cause de l'unicité des solutions d'une équation
différentielle, il faut bien que
. A cause de l'unicité des solutions d'une équation
différentielle, il faut bien que
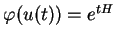 dans ce voisinage. On obtient
dans ce voisinage. On obtient 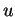 comme solution d'une équation différentielle qui est en quelque sorte l'équivalent de (7) aux niveau du paramétrage. Dans un second temps, on utilise la propriété suivante
de l'exponentielle pour montrer que
comme solution d'une équation différentielle qui est en quelque sorte l'équivalent de (7) aux niveau du paramétrage. Dans un second temps, on utilise la propriété suivante
de l'exponentielle pour montrer que 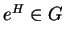 (5.4).
(5.4).
a)Il existe
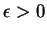 tel que
tel que
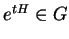 lorsque
lorsque
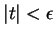 .
.
Choisissons donc un paramétrage
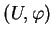 d'un voisinage de
d'un voisinage de 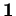 dans
dans 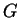 et
posons
et
posons
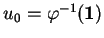 .
.
Notons 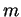 l'expression de la multiplication dans ce paramétrage:
l'expression de la multiplication dans ce paramétrage:
Cette fonction est définie pour 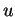 et
et 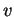 dans un voisinage
dans un voisinage 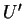 de
de 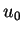 choisi pour que le produit
choisi pour que le produit
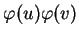 appartienne à la partie de
appartienne à la partie de 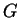 décrite par le paramétrage,
décrite par le paramétrage,
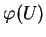 . La fonction
. La fonction 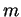 est d'ailleurs de classe
est d'ailleurs de classe
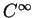 . En effet, on peut supposer que
. En effet, on peut supposer que 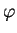 est de classe
est de classe
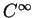 (5.5) et, de plus, supposer que c'est un paramétrage par des coordonnées (cela simplifie les choses mais la propriété est vraie pour tout paramétrage). Il est alors évident que
(5.5) et, de plus, supposer que c'est un paramétrage par des coordonnées (cela simplifie les choses mais la propriété est vraie pour tout paramétrage). Il est alors évident que
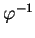 est de classe
est de classe
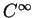 et donc que
et donc que 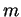 l'est aussi puisque la multiplication des matrices l'est également:
l'est aussi puisque la multiplication des matrices l'est également:
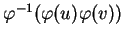 consiste à prendre certaines des composantes de
consiste à prendre certaines des composantes de
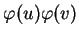 .
.
Pour illustrer ce que représente 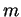 sur un exemple, considérons le paramétrage
sur un exemple, considérons le paramétrage
de
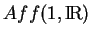 . Les paramètres de
. Les paramètres de 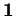 sont
sont 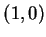 et la fonction
et la fonction 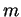 est
est
Notons 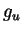 l'application
l'application
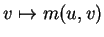 et posons
et posons
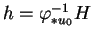 (5.6).
L'équation différentielle
(5.6).
L'équation différentielle
admet une solution
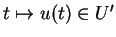 définie dans un intervalle
définie dans un intervalle
![$ ]-\epsilon,\epsilon[$](img870.gif) , où elle est par ailleurs unique. Son image
, où elle est par ailleurs unique. Son image
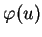 par le paramétrage est une solution de
(7). En effet,
par le paramétrage est une solution de
(7). En effet,
Considérons une courbe
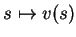 de
de 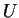 passant par
passant par 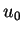 et
tangente à
et
tangente à 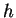 en
en 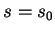 , par exemple
, par exemple 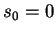 et
et
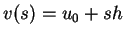 . La
courbe
. La
courbe
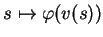 tracée sur
tracée sur
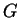 passe par
passe par 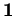 et est tangente à
et est tangente à 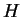 en
en 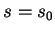 .
Par conséquent,
.
Par conséquent,
car
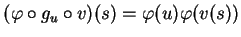 . Comme
. Comme
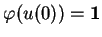 ,
,
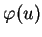 est bien solution de (7). Par conséquent,
est bien solution de (7). Par conséquent,
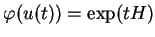 pour
pour 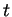 assez petit.
assez petit.
Dans le cas du groupe
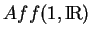 , on vérifie que si
, on vérifie que si
alors 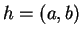 et que
et que
L'équation différentielle obtenue s'écrit donc, dans ce cas, sous la forme du système
Sa solution est immédiate. Nous obtenons
si 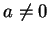 et
et
b)Conclusion de la démonstration.
On peut choisir un entier positif 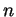 pour que
pour que
![$ 1/n\in]\epsilon,-\epsilon[$](img898.gif) . Pour un tel
. Pour un tel 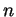 ,
,
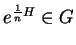 .
Nous pouvons donc décomposer
.
Nous pouvons donc décomposer
en un produit d'éléments de 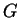 , ce qui montre qu'il en est un lui
aussi.
, ce qui montre qu'il en est un lui
aussi.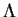
Dans certains cas particuliers, la connaissance explicite de
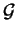 permet de vérifier directement que les exponentielles
permet de vérifier directement que les exponentielles
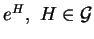 , appartiennent à
, appartiennent à 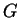 , en
utilisant le comportement de
, en
utilisant le comportement de 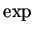 vis-à-vis des opérations
matricielles. Par exemple la formule
vis-à-vis des opérations
matricielles. Par exemple la formule
montre que l'exponentielle d'une matrice de trace nulle est une
matrice de déterminant 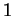 , etc.
, etc.
Sous-sections



suivant: 5.2.1.1 Illustration
monter: 5.2 Espace tangent aux
précédent: 5.2 Espace tangent aux
Table des matières
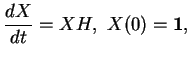
![]() tel que
tel que
![]() lorsque
lorsque
![]() .
.
![]() d'un voisinage de
d'un voisinage de ![]() dans
dans ![]() et
posons
et
posons
![]() .
.
![]() l'expression de la multiplication dans ce paramétrage:
l'expression de la multiplication dans ce paramétrage:
sur un exemple, considérons le paramétrage
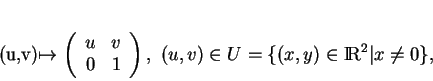
. Les paramètres de
sont
et la fonction
est
![]() l'application
l'application
![]() et posons
et posons
![]() (5.6).
L'équation différentielle
(5.6).
L'équation différentielle
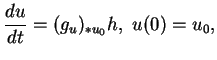
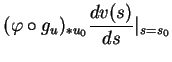
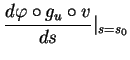
, on vérifie que si
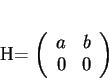
et que
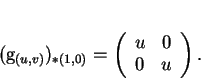
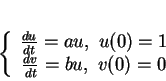
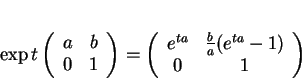
et
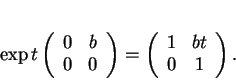
![]() pour que
pour que
![]() . Pour un tel
. Pour un tel ![]() ,
,
![]() .
Nous pouvons donc décomposer
.
Nous pouvons donc décomposer
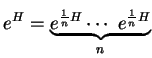
permet de vérifier directement que les exponentielles
, appartiennent à
, en utilisant le comportement de
vis-à-vis des opérations matricielles. Par exemple la formule
, etc.