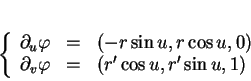suivant: 6.1.5.1 Première forme fondamentale
monter: 6.1 La première forme
précédent: 6.1.4 Distances & géodésiques
Table des matières
Dans
 , une surface de révolution est une union de cercles contenus dans des plans parallèles et centrés sur une droite perpendiculaires à ces plans, l'axe de révolution. Les cercles en question sont les parallèles de la surface et ses méridiens sont ses intersections avec les demi-plans délimités par l'axe de révolution.
, une surface de révolution est une union de cercles contenus dans des plans parallèles et centrés sur une droite perpendiculaires à ces plans, l'axe de révolution. Les cercles en question sont les parallèles de la surface et ses méridiens sont ses intersections avec les demi-plans délimités par l'axe de révolution.
Dans ce qui suit, nous considérons une surface de révolution  obtenue par la rotation autour de l'axe
obtenue par la rotation autour de l'axe
 d'une courbe
d'une courbe
 de la forme
de la forme
où la fonction 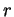 est au moins deux fois continûment dérivable dans l'intervalle
est au moins deux fois continûment dérivable dans l'intervalle ![$ I=]a,b[$](img1247.gif) et à valeurs strictement positives.
et à valeurs strictement positives.
Un point 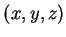 appartient à
appartient à  si et seulement si
si et seulement si
Comme
ne s'annule pas sur  , cette dernière est bien une variété plongée, définie par l'équation cartésienne
, cette dernière est bien une variété plongée, définie par l'équation cartésienne
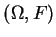 , où
, où 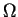 est l'ouvert
est l'ouvert
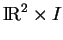 de
de
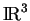 .
.
Nous allons vérifier que  admet des paramétrages
admet des paramétrages
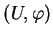 où
où
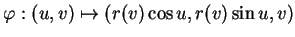 |
(6.3) |
et où 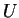 est de la forme
est de la forme
![$ ]u_0,u_0+2\pi[\times I.$](img1253.gif) Un tel paramétrage décrit
Un tel paramétrage décrit  à l'exception d'un méridien. L'application
à l'exception d'un méridien. L'application  est manifestement injective dans
est manifestement injective dans 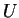 . On a
En particulier,
Par conséquent,
. On a
En particulier,
Par conséquent,
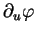 et
et
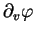 sont linéairement indépendants et
sont linéairement indépendants et
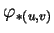 est injectif en chaque
est injectif en chaque
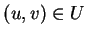 .
Il reste à voir que l'application réciproque de
.
Il reste à voir que l'application réciproque de  est continue. Or si
alors
est continue. Or si
alors 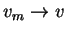 et, puisque
et, puisque 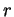 ne s'annule pas,
Par conséquent, on a aussi
ne s'annule pas,
Par conséquent, on a aussi 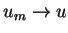 , ce qui prouve la continuité demandée(6.6).
, ce qui prouve la continuité demandée(6.6).
Sous-sections




suivant: 6.1.5.1 Première forme fondamentale
monter: 6.1 La première forme
précédent: 6.1.4 Distances & géodésiques
Table des matières
![]() obtenue par la rotation autour de l'axe
obtenue par la rotation autour de l'axe
![]() d'une courbe
d'une courbe
![]() de la forme
de la forme
![]() appartient à
appartient à ![]() si et seulement si
si et seulement si
![]() admet des paramétrages
admet des paramétrages
![]() où
où