



suivant: 6.1.6.3 Mesure des aires
monter: 6.1.6 Mesure des aires
précédent: 6.1.6.1 Produit mixte
Table des matières
Dans ce paragraphe, nous noterons 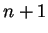 la dimension de l'espace vectoriel
la dimension de l'espace vectoriel  par ailleurs encore supposé
euclidien et orienté. Nous allons généraliser la notion de produit vectoriel introduite d'ordinaire
pour les espaces de dimension
par ailleurs encore supposé
euclidien et orienté. Nous allons généraliser la notion de produit vectoriel introduite d'ordinaire
pour les espaces de dimension 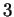 .
.
Proposition 44
Pour tous
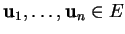
, il existe un seul
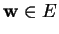
tel
que
Il ne saurait en exister qu'un seul. En effet, si
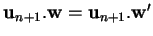 pour tout
pour tout
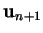 , alors
, alors
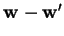 est perpendiculaire à
est perpendiculaire à  et est donc
nul. Dans une base orthonormée positive de
et est donc
nul. Dans une base orthonormée positive de  ,
,
![% latex2html id marker 20693
$ [{\bf u}_1,\ldots,{\bf u}_{n+1}]$](img1354.gif) est le déterminant de la matrice
est le déterminant de la matrice 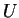 dont
les colonnes successives sont les composantes
de
dont
les colonnes successives sont les composantes
de
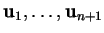 dans cette base:
où
dans cette base:
où
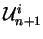 est le mineur algébrique de l'élément occupant
la dernière colonne et la
est le mineur algébrique de l'élément occupant
la dernière colonne et la 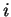 -ème ligne de
-ème ligne de 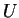 .
Le vecteur
.
Le vecteur 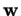 dont ces mineurs sont les composantes dans la base
considérée répond donc à la question.
dont ces mineurs sont les composantes dans la base
considérée répond donc à la question.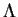
Le vecteur 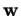 de l'énoncé précédent s'appelle le produit
vectoriel des
de l'énoncé précédent s'appelle le produit
vectoriel des 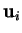 . On le note
. On le note
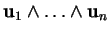 .
La démonstration de cet énoncé montre que, dans toute base
orthonormée positive de
.
La démonstration de cet énoncé montre que, dans toute base
orthonormée positive de  , sa composante numéro
, sa composante numéro 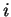 , exprimée à
l'aide des composantes
, exprimée à
l'aide des composantes 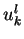 des
des
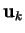 , est
, est
(les crochets signalent que les composantes de 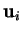 sont omises).
sont omises).
Proposition 45
a)
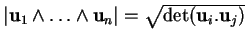
:
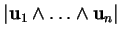
est le volume du paralléllépipède
engendré par les
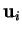
calculé
dans tout hyperplan qui les contient (
6.9).
b)
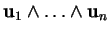
est nul si et
seulement si
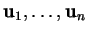
sont linéairement dépendants.
c)
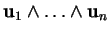
est orthogonal à chaque
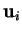
.
d) Si
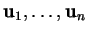
sont linéairement indépendants, alors
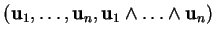
est une base
positive de

.
b) découle de a) car le volume en question est nul si et
seulement si les 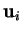 sont linéairement dépendants. Pour c), on
remarque que
est nul puisque deux arguments de ce produit mixte sont égaux. Quant
à d), il résulte de b) et de
Montrons a). Soit un hyperplan
sont linéairement dépendants. Pour c), on
remarque que
est nul puisque deux arguments de ce produit mixte sont égaux. Quant
à d), il résulte de b) et de
Montrons a). Soit un hyperplan 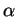 contenant les
contenant les 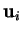 . (Il
est unique si ceux-ci sont linéairement dépendants.)
On choisit une base orthonormée positive
. (Il
est unique si ceux-ci sont linéairement dépendants.)
On choisit une base orthonormée positive
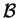 de
de  dont les
dont les 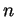 premiers éléments forment une base
premiers éléments forment une base
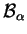 de
de 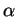 .
Calculé dans la base
.
Calculé dans la base
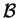 ,
,
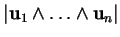 est la
valeur absolue du déterminant de la matrice des composantes des
est la
valeur absolue du déterminant de la matrice des composantes des
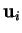 dans la base
dans la base
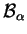 de
de 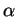 , c'est-à-dire la valeur absolue de leur
produit mixte calculé dans l'espace vectoriel
, c'est-à-dire la valeur absolue de leur
produit mixte calculé dans l'espace vectoriel 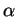 orienté par
cette base. D'où le résultat,
en appliquant la Proposition 43.
orienté par
cette base. D'où le résultat,
en appliquant la Proposition 43.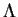
Lorsque 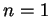 , le produit vectoriel n'a qu'un argument. C'est une
application linéaire
, le produit vectoriel n'a qu'un argument. C'est une
application linéaire
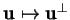 de
de  dans lui-même.
Si
dans lui-même.
Si
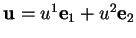 , alors
, alors
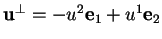 , la base
, la base
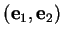 étant orthonormée positive. C'est la
rotation vectorielle
d'angle
étant orthonormée positive. C'est la
rotation vectorielle
d'angle 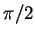 . En particulier,
. En particulier,
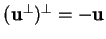 .
.




suivant: 6.1.6.3 Mesure des aires
monter: 6.1.6 Mesure des aires
précédent: 6.1.6.1 Produit mixte
Table des matières
![% latex2html id marker 20699
$\displaystyle [{\bf u}_1,\ldots,{\bf u}_{n+1}]=\sum_i{\bf u}_{n+1}^i{\mathcal U}_{n+1}^i,
$](img1356.gif)
![]() de l'énoncé précédent s'appelle le produit
vectoriel des
de l'énoncé précédent s'appelle le produit
vectoriel des ![]() . On le note
. On le note
![]() .
La démonstration de cet énoncé montre que, dans toute base
orthonormée positive de
.
La démonstration de cet énoncé montre que, dans toute base
orthonormée positive de ![]() , sa composante numéro
, sa composante numéro ![]() , exprimée à
l'aide des composantes
, exprimée à
l'aide des composantes ![]() des
des
![]() , est
, est
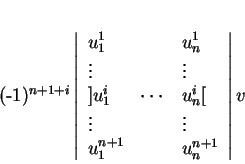
![]() , le produit vectoriel n'a qu'un argument. C'est une
application linéaire
, le produit vectoriel n'a qu'un argument. C'est une
application linéaire
![]() de
de ![]() dans lui-même.
Si
dans lui-même.
Si
![]() , alors
, alors
![]() , la base
, la base
![]() étant orthonormée positive. C'est la
rotation vectorielle
d'angle
étant orthonormée positive. C'est la
rotation vectorielle
d'angle ![]() . En particulier,
. En particulier,
![]() .
.