suivant: 6.1.6.2 Produit vectoriel
monter: 6.1.6 Mesure des aires
précédent: 6.1.6 Mesure des aires
Table des matières
Nous désignons par  un espace vectoriel
(réel) de dimension
un espace vectoriel
(réel) de dimension
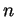 . Il est euclidien et orienté.
. Il est euclidien et orienté.
Lemme 42
Le déterminant
dont les colonnes sont formées par les composantes
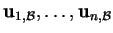
de
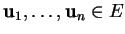
dans
une base
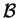
de

prend la même valeur dans toutes les bases orthonormées positives.
En effet, on passe d'une base orthonormée positive
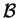 à une
base orthonormée positive
à une
base orthonormée positive
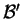 au moyen d'une matrice
au moyen d'une matrice 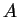 orthogonale et de déterminant
orthogonale et de déterminant  .
On a alors
.
On a alors
La valeur que prend le déterminant du lemme ci-dessus dans les bases
orthonormées positives de  s'appelle le produit mixte des
vecteurs
s'appelle le produit mixte des
vecteurs 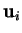 .
Il est noté
.
Il est noté
![% latex2html id marker 20610
$ [{\bf u}_1,\ldots,{\bf u}_n]$](img1323.gif) . Voici son interprétation
géométrique.
. Voici son interprétation
géométrique.
Supposons d'abord les 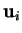 linéairement indépendants.
Le parallélépipède en question est, par définition, l'ensemble
L'application
linéairement indépendants.
Le parallélépipède en question est, par définition, l'ensemble
L'application
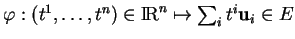 est un paramétrage.
Il transforme
est un paramétrage.
Il transforme ![$ [0,1]^n$](img1330.gif) en
en
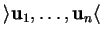 . Le
volume de celui-ci est donc(6.7)
par la formule du changement de variables dans les intégrales.
Lorsque les
. Le
volume de celui-ci est donc(6.7)
par la formule du changement de variables dans les intégrales.
Lorsque les 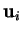 sont linéairement dépendants les deux membres extrêmes de ces égalités sont nuls.
D'autre part, si nous notons
sont linéairement dépendants les deux membres extrêmes de ces égalités sont nuls.
D'autre part, si nous notons 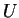 la matrice dont les colonnes sont
les composantes des
la matrice dont les colonnes sont
les composantes des 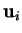 dans la base du repère, alors, puisque ce
dernier est orthonormé,
dans la base du repère, alors, puisque ce
dernier est orthonormé,
Au passage, observons que la dernière égalité démontre que l'on a
toujours
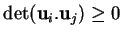 , l'égalité ayant lieu si et
seulement les
, l'égalité ayant lieu si et
seulement les 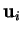 sont linéairement dépendants. Remarquons aussi
que
sont linéairement dépendants. Remarquons aussi
que
ce qui montre que le volume de
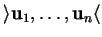 s'exprime à l'aide des longueurs,
s'exprime à l'aide des longueurs,
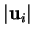 et
et
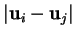 des côtés du simplexe
(6.8)
Ceci permet par exemple d'écrire le volume d'un tétraèdre en terme
des longueurs de ses arêtes (cas
des côtés du simplexe
(6.8)
Ceci permet par exemple d'écrire le volume d'un tétraèdre en terme
des longueurs de ses arêtes (cas 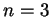 ) et de retrouver la formule de
Héron
exprimant la surface d'un triangle dont les côtés sont de longueurs
) et de retrouver la formule de
Héron
exprimant la surface d'un triangle dont les côtés sont de longueurs
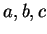 et de demi périmètre
et de demi périmètre 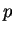 (cas
(cas 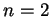 ).
).
Tout espace vectoriel euclidien de dimension finie possède donc un
produit mixte associé à chacune de ses deux orientations possibles.
C'est en particulier le
cas des sous-espaces vectoriels d'un tels espace car ils héritent de
son produit scalaire et sont donc euclidiens. Nous allons voir que
les produits mixtes des
hyperplans vectoriels d'un espace sont liés au produit vectoriel
défini sur celui-ci.




suivant: 6.1.6.2 Produit vectoriel
monter: 6.1.6 Mesure des aires
précédent: 6.1.6 Mesure des aires
Table des matières
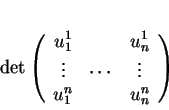
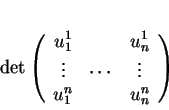
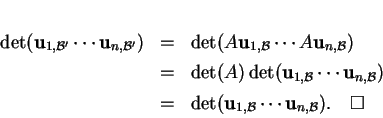
![]() s'appelle le produit mixte des
vecteurs
s'appelle le produit mixte des
vecteurs ![]() .
Il est noté
.
Il est noté
![]() . Voici son interprétation
géométrique.
. Voici son interprétation
géométrique.
![\begin{displaymath}
% latex2html id marker 20631\begin{array}{cll}
mes(\rangle...
...\\ [1ex]
&=&\vert[{\bf u}_1,\ldots,{\bf u}_n]\vert
\end{array}\end{displaymath}](img1332.gif)
![]() , l'égalité ayant lieu si et
seulement les
, l'égalité ayant lieu si et
seulement les ![]() sont linéairement dépendants. Remarquons aussi
que
sont linéairement dépendants. Remarquons aussi
que