



suivant: 5.2.2.3 L'algèbre de Lie
monter: 5.2.2 L'algèbre de Lie
précédent: 5.2.2.1 Algèbres de Lie
Table des matières
Proposition 29
Si
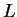
est une algèbre de Lie de dimension
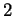
non commutative, alors
elle est isomorphe à
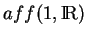
: elle admet une base
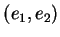
pour laquelle
![$ [e_1,e_2]=e_2$](img965.gif)
.
Soit une base 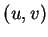 de
de 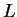 . Si
. Si 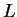 n'est pas commutatif, le
crochet
n'est pas commutatif, le
crochet
![$ [u,v]=au+bv$](img966.gif) n'est pas nul. Supposons par exemple que
n'est pas nul. Supposons par exemple que 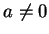 .
On a donc
La base
.
On a donc
La base
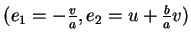 est alors telle que
est alors telle que
![$ [e_1,e_2]=e_2$](img965.gif) .
Pour conclure, on observe que la base
de
.
Pour conclure, on observe que la base
de
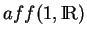 est telle que
est telle que
![$ [e'_1,e'_2]=e'_2$](img971.gif) .
.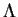
Il y a, à isomorphisme près, une dizaine de familles d'algèbres de Lie de
dimension 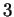 . Outre l'algèbre commutative, il y a l'algèbre de Lie de Heisenberg
. Outre l'algèbre commutative, il y a l'algèbre de Lie de Heisenberg
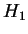 (voir plus bas la définition de
(voir plus bas la définition de 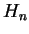 ), le produit
), le produit
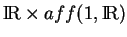 (5.10),
(5.10), 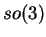 et
et
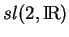 . Les deux dernières admettent une base
. Les deux dernières admettent une base
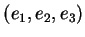 telle que, respectivement,
telle que, respectivement,
et
Pour rappel,
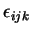 vaut
vaut  ou
ou 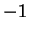 selon que
selon que 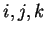 est
une permutation paire ou impaire de
est
une permutation paire ou impaire de 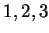 et est nul sinon.
et est nul sinon.
Si on rapporte un espace vectoriel euclidien orienté  de dimension
de dimension
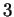 à une base orthonormée positive
à une base orthonormée positive
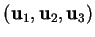 , alors
, alors
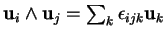 . Le produit vectoriel fait donc de
. Le produit vectoriel fait donc de  une
algèbre de Lie isomorphe à
une
algèbre de Lie isomorphe à 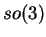 . On peut y vérifier directement
l'identité de Jacobi en
utilisant la formule du double produit vectoriel.
. On peut y vérifier directement
l'identité de Jacobi en
utilisant la formule du double produit vectoriel.




suivant: 5.2.2.3 L'algèbre de Lie
monter: 5.2.2 L'algèbre de Lie
précédent: 5.2.2.1 Algèbres de Lie
Table des matières
![$\displaystyle [u+\frac{b}{a}v,\frac{v}{a}]=u+\frac{b}{a}v.
$](img967.gif)
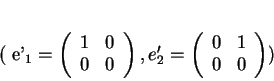
![]() . Outre l'algèbre commutative, il y a l'algèbre de Lie de Heisenberg
. Outre l'algèbre commutative, il y a l'algèbre de Lie de Heisenberg
![]() (voir plus bas la définition de
(voir plus bas la définition de ![]() ), le produit
), le produit
![]() (5.10),
(5.10), ![]() et
et
![]() . Les deux dernières admettent une base
. Les deux dernières admettent une base
![]() telle que, respectivement,
telle que, respectivement,
![$\displaystyle [e_i,e_j]=\sum_k\epsilon_{ijk}e_k
$](img977.gif)
de dimension
à une base orthonormée positive
, alors
. Le produit vectoriel fait donc de
une algèbre de Lie isomorphe à
. On peut y vérifier directement l'identité de Jacobi en utilisant la formule du double produit vectoriel.