


suivant: 3.2 Groupes de matrices
monter: 3.1 Les quadriques
précédent: 3.1.1 Premières propriétés
Table des matières
Nous n'aborderons que très succintement la classification des quadriques(3.1).
L'application 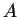 étant symétrique, on peut trouver une base dans laquelle elle est représentée par une matrice diagonale. Ainsi, un changement linéaire de coordonnées donne à
étant symétrique, on peut trouver une base dans laquelle elle est représentée par une matrice diagonale. Ainsi, un changement linéaire de coordonnées donne à 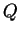 une équation de la forme
une équation de la forme
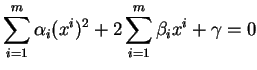 |
(3.1) |
que des changements de coordonnées affines supplémentaires permettent de simplifier jusqu'à l'obtention d'une forme canonique caractéristique de la quadrique.
Si, dans (4), 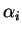 est non nul, alors on peut supposer que le coefficient
est non nul, alors on peut supposer que le coefficient 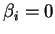 .
.
En effet, les termes de (4) où figure 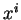 s'écrivent
s'écrivent
Le changement de coordonnées dans lequel 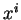 est remplacé par
est remplacé par
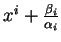 , une translation, annule
, une translation, annule 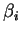 , modifie
, modifie 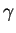 mais ne change aucun autre coefficient de (4).
mais ne change aucun autre coefficient de (4).
Ceci nous ramène à une équation du type
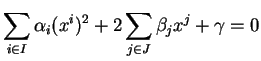 |
(3.2) |
dans laquelle aucun des
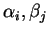 n'est nul et les ensembles d'indices
n'est nul et les ensembles d'indices
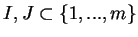 sont disjoints.
sont disjoints.
Le premier n'est pas vide car 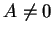 . Quitte à permuter les
. Quitte à permuter les 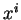 (3.2), on peut donc supposer que
(3.2), on peut donc supposer que
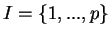 . Le nombre
. Le nombre 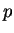 est le rang de
est le rang de 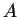 .
Si
.
Si
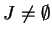 , alors on peut faire en sorte que
, alors on peut faire en sorte que 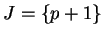 et
et 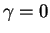 .
.
De fait, si
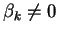 , le changement de coordonnées dans lequel
, le changement de coordonnées dans lequel 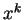 est remplacé par
est remplacé par
substitue 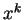 à ces termes dans (5). Au prix d'une permutation des coordonnées, on peut de plus supposer que
à ces termes dans (5). Au prix d'une permutation des coordonnées, on peut de plus supposer que 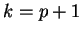 .
.
En fin de compte, on est ramené à trois sortes d'équations. Elles décrivent trois familles disjointes de quadriques.
La première correspond à
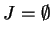 et
et
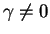 et contient les quadriques ayant un centre et pas de point double.
La deuxième correpond à
et contient les quadriques ayant un centre et pas de point double.
La deuxième correpond à 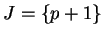 et contient les quadriques n'ayant pas de centre.
La dernière contient les quadriques ayant un point double. Elle est caractérisée par
et contient les quadriques n'ayant pas de centre.
La dernière contient les quadriques ayant un point double. Elle est caractérisée par
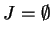 et
et 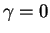 .
.
Un cylindre est une union de droites parallèles à une direction donnée, ses génératrices. Les solutions d'un système d'équations
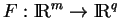 ne dépendant pas de variables
ne dépendant pas de variables
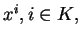 forment un cylindre admettant des génératrices parallèles à toute combinaison linéaire
forment un cylindre admettant des génératrices parallèles à toute combinaison linéaire 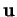 des
des
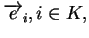 car, si
car, si 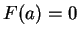 alors
alors
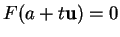 pour tout
pour tout 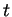 .
.
Une quadrique 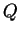 pour laquelle
pour laquelle 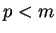 et
et
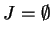 , ou
, ou 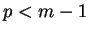 et
et
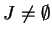 est donc un cylindre. Le nombre
est donc un cylindre. Le nombre 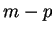 , ou
, ou 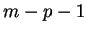 selon les cas est la dimension de l'espace des directions cylindriques de
selon les cas est la dimension de l'espace des directions cylindriques de 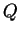 . Ce sont les directions auxquelles sont parallèles des génératrices de
. Ce sont les directions auxquelles sont parallèles des génératrices de 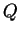 .
.
Dans
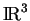 , si on s'en tient aux quadriques non vides qui ne sont ni des cônes ni des cylindres, alors il reste cinq sortes de quadriques.
, si on s'en tient aux quadriques non vides qui ne sont ni des cônes ni des cylindres, alors il reste cinq sortes de quadriques.
Ellipsoïde
 |
Hyperboloïdes à une nappe et à deux nappes

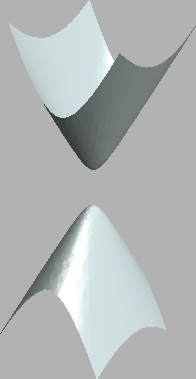 |
Paraboloïdes elliptique et hyperbolique

 |
Les trois premières sont des quadriques à centre: ellipsoïde, hyperboloïde à une nappe et hyperboloïde à deux nappes. Elles admettent les équations canoniques respectives
Les deux autres sont des quadriques sans centre: paraboloïde elliptique et paraboloïde hyperbolique dont les équations canoniques sont
respectivement. Dans ces expressions, 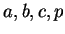 sont des nombres positifs.
sont des nombres positifs.



suivant: 3.2 Groupes de matrices
monter: 3.1 Les quadriques
précédent: 3.1.1 Premières propriétés
Table des matières
![]() est non nul, alors on peut supposer que le coefficient
est non nul, alors on peut supposer que le coefficient ![]() .
.
s'écrivent
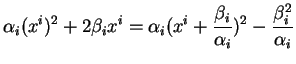
est remplacé par
, une translation, annule
, modifie
mais ne change aucun autre coefficient de (4).
![]() . Quitte à permuter les
. Quitte à permuter les ![]() (3.2), on peut donc supposer que
(3.2), on peut donc supposer que
![]() . Le nombre
. Le nombre ![]() est le rang de
est le rang de ![]() .
Si
.
Si
![]() , alors on peut faire en sorte que
, alors on peut faire en sorte que ![]() et
et ![]() .
.
, le changement de coordonnées dans lequel
est remplacé par
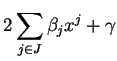
à ces termes dans (5). Au prix d'une permutation des coordonnées, on peut de plus supposer que
.
ne dépendant pas de variables
forment un cylindre admettant des génératrices parallèles à toute combinaison linéaire
des
car, si
alors
pour tout
.
![]() , si on s'en tient aux quadriques non vides qui ne sont ni des cônes ni des cylindres, alors il reste cinq sortes de quadriques.
, si on s'en tient aux quadriques non vides qui ne sont ni des cônes ni des cylindres, alors il reste cinq sortes de quadriques.
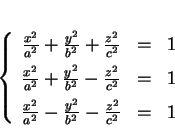
![\begin{displaymath}
% latex2html id marker 17581\left\{
\begin{array}{ccc}
\fr...
...[1ex]
\frac{x^2}{a^2}-\frac{y^2}{b^2}&=&2pz
\end{array}\right.
\end{displaymath}](img478.gif)