- ... (2.1
- Restreindre à
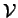 les translations de vecteur
les translations de vecteur
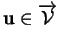 fait de
fait de
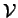 un espace affine sur
un espace affine sur
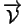 . La notation
. La notation
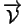 et la définition de
et la définition de
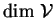 sont donc licites.
sont donc licites.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (2.2
- Les points sont les variétés affines de dimension 0.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (3.1
- On l'appelle aussi norme de
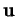 , et on le note aussi
, et on le note aussi
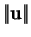 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rectangles(3.2
- et en anticipant un rien sur le chapitre
suivant
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...3.3
- sous réserve que
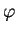 ne
soit ni 0 ni
ne
soit ni 0 ni 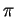 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (3.4
- Vu la Remarque 4.7, ces bases ont deux à deux
la même orientation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (4.1
- Par extension, on dit aussi que
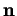 est une
normale à
est une
normale à  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (4.2
- Comprendre: la meilleure borne inférieure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(4.3
- En effet, le problème se ramène au cas précédent en considérant un plan contenant
 et
et

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (4.4
- Elle est forcément unique : s'il y a deux
perpendiculaires à
 et
et
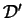 , elles forment nécessairement un
plan contenant
, elles forment nécessairement un
plan contenant
 et
et
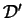 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...angperp(4.5
- La vérification de l'hypothèse d'orientation est facile mais fastidieuse; nous l'omettrons.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... latitude(4.6
- Elle diffère de la latitude géographique qui est mesurée à
partir de l'équateur plutôt qu'à partir du pôle nord.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (5.1
- Lorsque
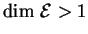 , cette propriété est
caractéristique des bijections affines. Nous ne nous servirons pas de ce fait, assez difficile à établir.
, cette propriété est
caractéristique des bijections affines. Nous ne nous servirons pas de ce fait, assez difficile à établir.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.2
- Les exemples considérés ici se généralisent facilement à des variétés
affines dont les sous-vectoriels directeurs sont supplémentaires l'un de l'autre.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.3
- Lorsque
 est orthogonale à
est orthogonale à  , il
s'agit de la projection orthogonale
, il
s'agit de la projection orthogonale
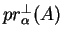 de
de  sur
sur  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrices(5.4
- C'est une façon de dire que le groupe des affinités de
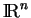 est un sous-groupe de celui des transformations linéaires de
est un sous-groupe de celui des transformations linéaires de
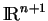 :
:
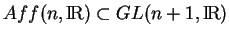
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.5
- On appelle de la même façon les autres
solutions des équations
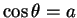 et
et
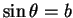 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.6
- On désigne par
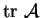 la trace de
l'application linéaire
la trace de
l'application linéaire
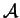 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ouvertes(6.1
- La boule ouverte de centre
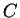 et rayon
et rayon 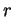 est l'ensemble des points dont la distance à
est l'ensemble des points dont la distance à 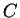 est plus petite que r.
est plus petite que r.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)(6.2
- Le mot paramétrage est réservé à des fonctions injectives. Nous ferons exception à cette règle pour les
paramétrages des arcs réguliers de courbes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(6.3
- Nous ne démontrerons pas ce fait qui repose sur le théorème des fonctions implicites.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(6.4
- Il s'agit bien d'une relation d'équivalence. La vérification est facile mais sans intérêt géométrique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.5
- Sauf pour une courbe plane, bien entendu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(6.6
- On obtiendrait aussi
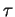 en calculant directement
en calculant directement 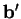 , mais c'est plus lourd.
, mais c'est plus lourd.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... donc(6.7
- La dérivée de l'inverse
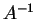 d'une matrice
d'une matrice  par rapport à une variable dont elle dépend est donnée par
par rapport à une variable dont elle dépend est donnée par
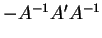 , où
, où 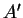 est
celle de
est
celle de  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.8
- Le cercle ne passant pas par
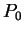 , on peut exclure celui-ci de
, on peut exclure celui-ci de 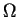 et garantir
ainsi que
et garantir
ainsi que
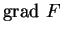 ne s'y annule pas.
ne s'y annule pas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.9
- L'arbitraire lié à l'orientation subsiste: si on remplace
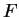 par
par 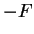 , on renverse
l'orientation.
, on renverse
l'orientation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.10
- Les calculs sont analogues lorsque l'ordonnée est le paramètre.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ci-dessus(6.11
- D'habitude, l'origine du repère est prise en le sommet de la
parabole, à mi-chemin entre le foyer et la directrice; avec
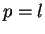 l'équation, canonique, de la parabole s'écrit alors
l'équation, canonique, de la parabole s'écrit alors 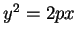 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inférieure(6.12
- c'est-à-dire celle
dont les points ont une ordonnée négative ou nulle dans le repère
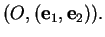
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (6.13
- Le signe de
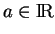 est ici
est ici 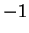 , 0 ou
, 0 ou 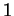 selon que
selon que 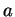 est respectivement négatif, nul ou
positif.
est respectivement négatif, nul ou
positif.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectivement(6.14
- Avec la première égalité, en posant
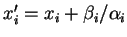 , on annule
, on annule
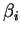 en conservant
en conservant 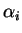 intact.
intact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.1
- Cette
définition est restrictive. En général, une surface est un ensemble
 dont chaque point possède un voisinage
dont chaque point possède un voisinage 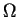 dans lequel est
définie une équation cartésienne de
dans lequel est
définie une équation cartésienne de
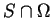 . Comme nous
n'abordons ici que l'étude locale des surface, il n'y a aucun problème
à adopter la définition moins générale du texte
. Comme nous
n'abordons ici que l'étude locale des surface, il n'y a aucun problème
à adopter la définition moins générale du texte
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... l'analyse(7.2
- Par exemple, le fait que la mesure de l'aire
obtenue par cette formule ne dépende pas du paramétrage est
une conséquence du théorème du changement de variables dans les
intégrales multiples.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cylindre(7.3
- En effet, la longueur d'un arc de cercle de rayon
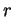 vu sous un angle
vu sous un angle 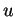 depuis le centre est
depuis le centre est 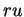 , pour autant que
l'angle soit mesuré en radians.
, pour autant que
l'angle soit mesuré en radians.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
cônes(7.4
- Un cône de sommet
 est un ensemble qui contient les
droites passant par
est un ensemble qui contient les
droites passant par  et ses points distincts de
et ses points distincts de  , appelées
génératrices.
, appelées
génératrices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cylindres(7.5
- Un cylindre est un ensemble qui contient les droites menées par ses points
parallèlement à une direction fixe donnée, appelées génératrices
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tenant(7.6
- comprendre connexe.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(7.7
- A titre d'exercice, on vérifiera que la surface décrite dans
l'exemple 2.1 est effectivement un paraboloïde hyperbolique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.8
- Nous ne donnerons pas la démonstration de ce fait, qui relève de
l'analyse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.9
- comprendre: pour
toute valeur de
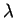
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(7.10
- Elle n'est définie que dans
l'ensemble des
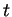 en lesquels
en lesquels
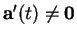 . Ce n'est pas nécessairement un arc régulier de courbe.
. Ce n'est pas nécessairement un arc régulier de courbe.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.