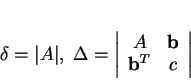suivant: 6.4.3.2.2 Discussion
monter: 6.4.3.2 Classification des courbes
précédent: 6.4.3.2 Classification des courbes
Table des matières
Un changement de repère modifie la forme de l'équation (30). On peut d'une part en profiter pour lui donner une forme simple. C'est la réduction à la
forme canonique de l'équation. On peut d'autre part essayer de détecter assez de quantités invariantes sous l'action du changement de repère pour pouvoir préciser
la nature du lieu considéré sans avoir à procéder à cette réduction.
Examinons comment se transforme l'équation lorsque l'on change la base du repère, passant ainsi de la coordonnée 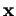 à
à 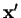 . On a
. On a
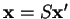 , où
, où  est une
matrice non singulière, qui est de plus orthogonale quand la nouvelle base est orthonormée comme l'ancienne. L'équation du lieu devient par conséquent
est une
matrice non singulière, qui est de plus orthogonale quand la nouvelle base est orthonormée comme l'ancienne. L'équation du lieu devient par conséquent
On en déduit que les déterminants
ne changent pas de signe (6.13) lors d'un changement de la base du repère. On vérifierait de même que ces déterminants sont inchangés par une translation de
l'origine du repère.




suivant: 6.4.3.2.2 Discussion
monter: 6.4.3.2 Classification des courbes
précédent: 6.4.3.2 Classification des courbes
Table des matières
2002-12-17
![]() à
à ![]() . On a
. On a
![]() , où
, où ![]() est une
matrice non singulière, qui est de plus orthogonale quand la nouvelle base est orthonormée comme l'ancienne. L'équation du lieu devient par conséquent
est une
matrice non singulière, qui est de plus orthogonale quand la nouvelle base est orthonormée comme l'ancienne. L'équation du lieu devient par conséquent