Remarque 6.2.2
Dans la suite, on désignera indifféremment par
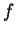
la fonction
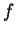
et sa représentation
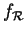
dans un repère
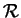
.
L'ambiguité qui peut résulter de cette convention est vénielle en regard de la simplification d'écriture qu'elle apporte.
Remarque 6.2.3
On est parfois amené à considérer des fonctions
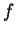
qui ne sont pas définies sur tout

, ou à restreindre une fonction à une partie
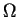
de

.
Dans ce cas, nous supposerons que
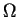
est un
ouvert de

, c'est-à-dire Ñ comme en analyse Ñ un ensemble qui est union de boules
ouvertes(
6.1). Dans un repère
orthonormé de

, les coordonnnées des points d'un tel ensemble décrivent un ouvert de
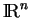
puisque le passage aux coordonnées conserve la distance.
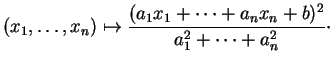
![]() à une droite d'équation paramétrique
à une droite d'équation paramétrique
![]() , on obtient une fonction d'une variable réelle
, on obtient une fonction d'une variable réelle ![]() dont il est
utile d'étudier la dérivabilité éventuelle.
dont il est
utile d'étudier la dérivabilité éventuelle.
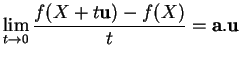
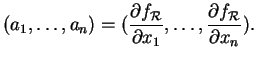
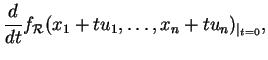
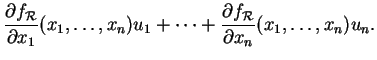
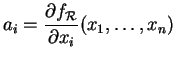
![]() est le gradient de
est le gradient de ![]() au point
au point ![]() . On le note
. On le note
![]() . Le nombre
. Le nombre
![]() est la dérivée de
est la dérivée de ![]() en
en ![]() dans la direction de
dans la direction de ![]() .
.