



suivant: 3.3.2 Orientation d'un plan
monter: 3.3 Orientation, en dimensions
précédent: 3.3 Orientation, en dimensions
Table des matières
Comment traduire ceci analytiquement?
Si on peut déformer de manière continue la base
 en la base
en la base
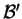 alors le déterminant de la matrice formée des composantes des éléments de
alors le déterminant de la matrice formée des composantes des éléments de
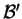 selon
selon
 (cf. Remarque 4.7) est positif: lorsque
(cf. Remarque 4.7) est positif: lorsque
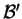 est proche de
est proche de
 , cette matrice est proche de l'identité. Son déterminant est donc proche de
, cette matrice est proche de l'identité. Son déterminant est donc proche de 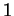 et est
positif. Il doit alors le rester durant toute la transformation car s'il changeait de signe, alors il s'annulerait, ce qui ne se peut. Inversement, on peut établir
que si le déterminant de la matrice représentant
et est
positif. Il doit alors le rester durant toute la transformation car s'il changeait de signe, alors il s'annulerait, ce qui ne se peut. Inversement, on peut établir
que si le déterminant de la matrice représentant
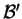 selon
selon
 est positif, alors on peut transformer continûment
est positif, alors on peut transformer continûment
 en
en
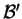 . Ceci nous amène à dire que
deux bases de
. Ceci nous amène à dire que
deux bases de  sont de même orientation si le déterminant de la matrice exprimant les éléments de l'une selon l'autre est positif. Orienter
sont de même orientation si le déterminant de la matrice exprimant les éléments de l'une selon l'autre est positif. Orienter  consiste à choisir une base et à ne rapporter
consiste à choisir une base et à ne rapporter  qu'à des bases de même orientation que celle-ci (3.4)(les bases choisies pour orienter
qu'à des bases de même orientation que celle-ci (3.4)(les bases choisies pour orienter  sont parfois dites positives).
sont parfois dites positives).
2002-12-17