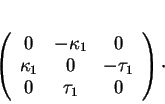suivant: 6.4 Courbes planes
monter: 6.3.2 Le trièdre de
précédent: 6.3.2.1 Tangente, normale principale
Table des matières
Il peut être utile de calculer ces éléments lorsque le paramétrage considéré
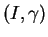 n'est pas naturel.
Pour simplifier les écritures, nous désignerons par
n'est pas naturel.
Pour simplifier les écritures, nous désignerons par 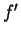 la dérivée d'une fonction
la dérivée d'une fonction 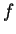 par rapport à l'argument
par rapport à l'argument 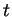 de
de 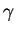 et, comme plus haut, par
et, comme plus haut, par 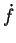 la dérivée par rapport à
la dérivée par rapport à 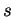 de cette fonction exprimée en terme d'une abscisse curviligne
de cette fonction exprimée en terme d'une abscisse curviligne 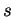 comptée positivement dans l'orientation associée à
comptée positivement dans l'orientation associée à 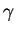 . La
règle de dérivation des fonctions composées donne la relation
. La
règle de dérivation des fonctions composées donne la relation
Proposition 6.3.12
Soient un arc paramétré de courbe

et un de ses paramétrages
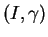
. Si
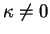
, on a
et
Preuve. En dérivant
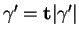 par rapport à
par rapport à 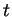 , on obtient
, on obtient
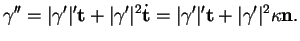 |
(6.5) |
D'autre part, en dérivant
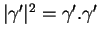 , il vient
Par conséquent
Les deux premières formules en découlent directement. La troisième est une conséquence immédiate de la première.
Pour calculer
, il vient
Par conséquent
Les deux premières formules en découlent directement. La troisième est une conséquence immédiate de la première.
Pour calculer 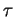 , multiplions vectoriellement par
, multiplions vectoriellement par 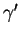 les membres de (27) puis dérivons par rapport à
les membres de (27) puis dérivons par rapport à 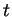 (6.6).
Il vient d'abord
puis
Tenant compte de l'expression trouvée plus haut pour
(6.6).
Il vient d'abord
puis
Tenant compte de l'expression trouvée plus haut pour 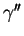 , cela donne successivement
D'où le résultat.
, cela donne successivement
D'où le résultat.
Exemple 6.3.13
Courbure et torsion de l'hélice circulaire (
24)
Pour cette hélice, on trouve facilement, en appliquant les formules qu'on vient d'établir,
Lorsque 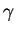 représente le paramétrage par le temps de la trajectoire d'un point matériel,
représente le paramétrage par le temps de la trajectoire d'un point matériel, 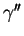 en est l'accélération.
La formule (27) montre que celle-ci se compose de deux termes: l'accélération tangentielle
en est l'accélération.
La formule (27) montre que celle-ci se compose de deux termes: l'accélération tangentielle
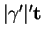 et l'accélération normale
et l'accélération normale
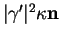 .
.
Proposition 6.3.14
Soit un arc régulier de courbe

admettant le paramétrage naturel
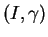
. Si
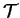
est une isométrie positive de
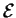
, alors
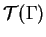
est un arc
régulier de courbe admettant le paramétrage naturel
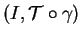
et, pour autant qu'elles soient définies, ses tangentes, normales principales
et binormales sont données par
où
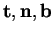
sont les éléments correspondants de

. De plus, la courbure et la torsion de
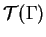
sont, comme fonctions de
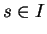
, égales aux
fonctions correspondantes de

.
Preuve. Notons 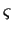 la fonction
la fonction
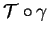 . Dans un repère orthonormé positif de
. Dans un repère orthonormé positif de
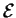 ,
,
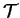 est représenté par
où
est représenté par
où 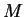 est la matrice orthogonale représentant
est la matrice orthogonale représentant
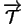 et
et
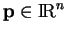 . En confondant
. En confondant
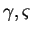 et leurs expressions en coordonnées, on a donc
ce qui se traduit par
Comme
et leurs expressions en coordonnées, on a donc
ce qui se traduit par
Comme
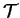 est une isométrie positive,
est une isométrie positive,
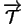 conserve les produits
mixtes et vectoriels. La Proposition 3.12 permet alors de conclure.
conserve les produits
mixtes et vectoriels. La Proposition 3.12 permet alors de conclure.

Remarque 6.3.15
Dans l'énoncé ci-dessus, si l'isométrie est négative, alors la normale et la courbure sont conservées; la tangente, la binormale et la torsion sont
remplacées par leurs opposés.
Les formules de Frenet montrent, inversement, qu'un arc régulier de courbe est déterminé à isométrie près par les fonctions 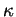 et
et 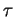 .
.
Proposition 6.3.16
Soient des arcs réguliers de courbes
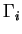
,
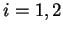
, admettant des paramétrages naturels
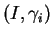
définis sur un intervalle ouvert
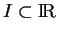
dans lequel les courbures
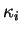
ne s'annulent pas. Si
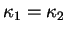
et
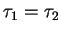
dans
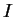
, alors il existe une isométrie
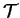
de
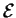
telle que
pour tout
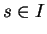
.
Preuve. Plaçons-nous dans un repère orthonormé positif. Dans celui-ci, les composantes des éléments du trièdre de Frenet
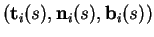 de
de 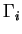 en
en
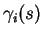 sont les colonnes d'une matrice orthogonale
sont les colonnes d'une matrice orthogonale 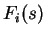 . Les formules de Frenet montrent que les matrices
. Les formules de Frenet montrent que les matrices 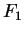 et
et 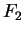 sont solutions de l'équation
où
sont solutions de l'équation
où 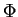 est la matrice
On a donc(6.7)
est la matrice
On a donc(6.7)
Par conséquent,
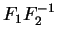 est une matrice constante, orthogonale et de déterminant positif
est une matrice constante, orthogonale et de déterminant positif 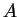 . Quitte à remplacer
. Quitte à remplacer 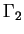 par son image par
l'isométrie représentée par
par son image par
l'isométrie représentée par
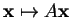 , on peut supposer que
, on peut supposer que 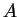 est la matrice unité et, par conséquent, que
est la matrice unité et, par conséquent, que 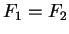 . En particulier,
Ayant même dérivée dans l'intervalle
. En particulier,
Ayant même dérivée dans l'intervalle 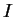 que
que 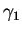 ,
, 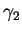 est donc le translaté de
est donc le translaté de 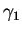 par la translation de vecteur
constant
par la translation de vecteur
constant
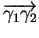 .
.





suivant: 6.4 Courbes planes
monter: 6.3.2 Le trièdre de
précédent: 6.3.2.1 Tangente, normale principale
Table des matières
2002-12-17
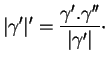
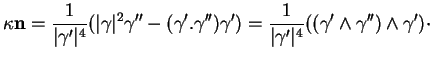
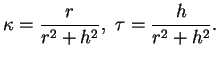
![]() représente le paramétrage par le temps de la trajectoire d'un point matériel,
représente le paramétrage par le temps de la trajectoire d'un point matériel, ![]() en est l'accélération.
La formule (27) montre que celle-ci se compose de deux termes: l'accélération tangentielle
en est l'accélération.
La formule (27) montre que celle-ci se compose de deux termes: l'accélération tangentielle
![]() et l'accélération normale
et l'accélération normale
![]() .
.
![]() et
et ![]() .
.