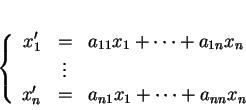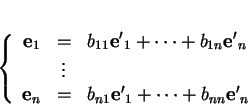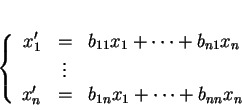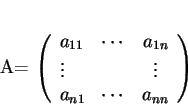suivant: 1.5 Sous-espaces vectoriels
monter: 1.4 Combinaisons linéaires, bases
précédent: 1.4.3 Composantes
Table des matières
Sauf pour
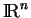 , il n'y a généralement pas de base privilégiée. Il importe donc de savoir changer de base
d'autant que, même dans
, il n'y a généralement pas de base privilégiée. Il importe donc de savoir changer de base
d'autant que, même dans
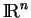 , cela peut être opportun afin de simplifier la formulation et
la résolution des problèmes que l'on étudie.
, cela peut être opportun afin de simplifier la formulation et
la résolution des problèmes que l'on étudie.
Soient des bases
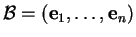 et
et
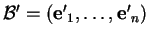 de
de  .
Notons
.
Notons
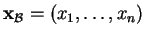 et
et
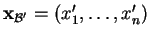 les composantes d'un élément quelconque
les composantes d'un élément quelconque 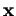 de
de  dans
ces bases respectivement. La question est de calculer les
dans
ces bases respectivement. La question est de calculer les 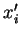 à l'aide des
à l'aide des 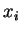 .
.
Proposition 1.4.6
Les composantes de
x selon
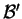
sont des fonctions homogènes du premier degré
en les composantes de
x selon

:
Ces fonctions sont indépendantes, en ce sens que les vecteurs formés par les coefficients des inconnues,
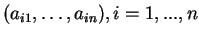
,
sont linéairement indépendants dans
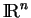
.
Preuve. Puisque
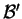 est une base, les éléments de
est une base, les éléments de
 sont des combinaisons linéaires de ceux de
sont des combinaisons linéaires de ceux de
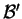 :
Par définition des composantes de x selon
:
Par définition des composantes de x selon
 , on a donc
, on a donc
Par conséquent,
sont de la forme indiquées, avec
Il reste à vérifier que les
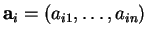 sont linéairement indépendants. Mais
si
alors, pour tout
sont linéairement indépendants. Mais
si
alors, pour tout
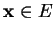 , on a
Avec
, on a
Avec 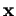 égal à
égal à
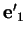 ,...,
,...,
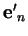 ,
on obtient alors
,
on obtient alors
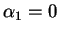 ,...,
,...,
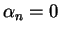 .
.

Remarque 1.4.7
Le tableau
est facile à construire. Sa colonne numéro
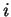
est formée des composantes de
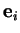
selon
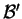
.
A l'aide du calcul matriciel, on peut donc encore écrire
où

est la matrice exprimant

dans la base
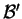
.
Souvent, c'est
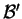
qui est donné dans la base

, au moyen d'une matrice
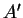
. On a alors
Si la matrice exprimant
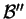
dans
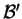
est
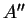
, alors celle qui décrit
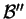
dans

est le produit
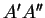
.
Remarque 1.4.8
Dans le tableau

ci-dessus, les colonnes sont linéairement indépendantes.
C'est en effet la condition sous laquelle les
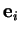
forment une base.
Il résulte donc de la Proposition
4.6 que si les colonnes d'un tableau carré sont linéairement indépendantes,
alors les lignes de ce tableau le sont aussi.




suivant: 1.5 Sous-espaces vectoriels
monter: 1.4 Combinaisons linéaires, bases
précédent: 1.4.3 Composantes
Table des matières
2002-12-17
![]() , il n'y a généralement pas de base privilégiée. Il importe donc de savoir changer de base
d'autant que, même dans
, il n'y a généralement pas de base privilégiée. Il importe donc de savoir changer de base
d'autant que, même dans
![]() , cela peut être opportun afin de simplifier la formulation et
la résolution des problèmes que l'on étudie.
, cela peut être opportun afin de simplifier la formulation et
la résolution des problèmes que l'on étudie.
![]() et
et
![]() de
de ![]() .
Notons
.
Notons
![]() et
et
![]() les composantes d'un élément quelconque
les composantes d'un élément quelconque ![]() de
de ![]() dans
ces bases respectivement. La question est de calculer les
dans
ces bases respectivement. La question est de calculer les ![]() à l'aide des
à l'aide des ![]() .
.