



suivant: 6.4.2.1 Equation de la
monter: 6.4 Courbes planes
précédent: 6.4.1 Graphe de fonction
Table des matières
On peut écrire
faisant ainsi apparaître la condition
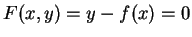 liant les coordonnées d'un point de
liant les coordonnées d'un point de
 pour qu'il appartienne à
pour qu'il appartienne à 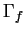 .
Cette relation est très simple car elle fournit explicitement l'une des coordonnées en fonction de l'autre. Pour un arc paramétré de courbe quelconque, on peut
encore espérer exprimer la condition nécessaire et suffisante que doivent satisfaire les coordonnées d'un point pour qu'il soit situé sur l'arc sous la forme d'une
équation implicite
.
Cette relation est très simple car elle fournit explicitement l'une des coordonnées en fonction de l'autre. Pour un arc paramétré de courbe quelconque, on peut
encore espérer exprimer la condition nécessaire et suffisante que doivent satisfaire les coordonnées d'un point pour qu'il soit situé sur l'arc sous la forme d'une
équation implicite 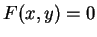 mais on doit s'attendre à ce qu'elle soit plus compliquée.
mais on doit s'attendre à ce qu'elle soit plus compliquée.
Dans le cas du cercle (23), on peut prendre
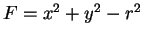 à laquelle on peut
donner localement la forme d'un graphe, en résolvant par rapport à
à laquelle on peut
donner localement la forme d'un graphe, en résolvant par rapport à 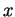 où à
où à 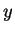 . Par exemple, la solution
. Par exemple, la solution
décrit les points du cercle dont l'ordonnée est positive ou nulle. Elle n'est pas prolongeable de manière dérivable dans un intervalle plus grand. Pour prendre en
compte toutes les solutions de l'équation
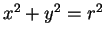 , il faut donc considérer plusieurs graphes.
, il faut donc considérer plusieurs graphes.
On démontre en analyse que si 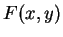 est de classe
est de classe 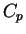 dans un ouvert
dans un ouvert
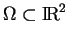 , et si
, et si
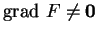 quand
quand 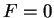 , alors s'il n'est pas vide,
l'ensemble
, alors s'il n'est pas vide,
l'ensemble
peut être localement paramétré par une des coordonnées, au moyen de fonctions de classe 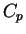 . Plus précisément il l'est par
. Plus précisément il l'est par 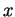 quand
quand
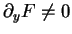 et par
et par 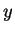 quand
quand
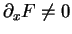 . De plus, les différents paramétrages obtenus sont localement équivalents. C'est donc une union
d'arcs paramétrés de courbes qui se raccordent sans discontinuité. Par extension, on appellera encore cet ensemble arc régulier de courbe. L'équation
. De plus, les différents paramétrages obtenus sont localement équivalents. C'est donc une union
d'arcs paramétrés de courbes qui se raccordent sans discontinuité. Par extension, on appellera encore cet ensemble arc régulier de courbe. L'équation 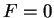 qui
traduit exactement les conditions que doivent vérifier les coordonnées d'un point de
qui
traduit exactement les conditions que doivent vérifier les coordonnées d'un point de  pour lui appartenir est une équation cartésienne de l'arc.
On appelle alors paramétrage local de
pour lui appartenir est une équation cartésienne de l'arc.
On appelle alors paramétrage local de  tout paramétrage
tout paramétrage
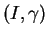 tel que
tel que
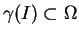 et
et
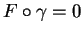 .
.
Exemple 6.4.3
Les droites
Une équation cartésienne 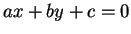 , au sens des chapitres précédents, d'une droite
, au sens des chapitres précédents, d'une droite
 est aussi une équation cartésienne au sens que l'on vient de définir:
on prend
est aussi une équation cartésienne au sens que l'on vient de définir:
on prend
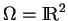 , dans lequel le gradient
, dans lequel le gradient 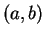 de
de
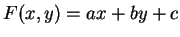 n'est pas nul.
n'est pas nul.
Exemple 6.4.4
Les cercles
Comme
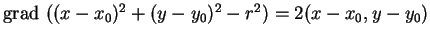 , la fonction
, la fonction
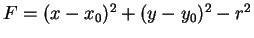 restreinte à
restreinte à
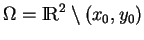 fournit une équation
cartésienne du cercle de rayon
fournit une équation
cartésienne du cercle de rayon 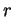 et de centre
et de centre
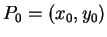 (6.8).
(6.8).
Si
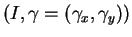 est un paramétrage local de
est un paramétrage local de 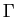 , alors en dérivant l'identité
, alors en dérivant l'identité
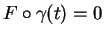 , on obtient
, on obtient
qui montre que
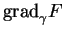 est orthogonal au vecteur tangent
est orthogonal au vecteur tangent 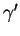 en
en 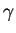 tandis que le vecteur de composantes
tandis que le vecteur de composantes
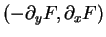 est un multiple
est un multiple  de
de 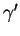 . Comme plus haut dans le cas du graphe d'une fonction, on peut donc obtenir des vecteurs tangent et normal à
. Comme plus haut dans le cas du graphe d'une fonction, on peut donc obtenir des vecteurs tangent et normal à 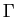 en
en
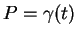 formant une base positive:
Selon le signe de
formant une base positive:
Selon le signe de  , ce sont les vecteurs correspondant de
, ce sont les vecteurs correspondant de 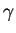 ou leurs opposés. Comme ils sont exprimés de manière indépendante de
ou leurs opposés. Comme ils sont exprimés de manière indépendante de 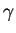 , nous
conviendrons d'orienter
, nous
conviendrons d'orienter 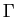 dans le sens de
dans le sens de 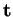 (6.9).
(6.9).
Sous-sections




suivant: 6.4.2.1 Equation de la
monter: 6.4 Courbes planes
précédent: 6.4.1 Graphe de fonction
Table des matières
2002-12-17
![]() à laquelle on peut
donner localement la forme d'un graphe, en résolvant par rapport à
à laquelle on peut
donner localement la forme d'un graphe, en résolvant par rapport à ![]() où à
où à ![]() . Par exemple, la solution
. Par exemple, la solution
![]() est de classe
est de classe ![]() dans un ouvert
dans un ouvert
![]() , et si
, et si
![]() quand
quand ![]() , alors s'il n'est pas vide,
l'ensemble
, alors s'il n'est pas vide,
l'ensemble
![]() , la fonction
, la fonction
![]() restreinte à
restreinte à
![]() fournit une équation
cartésienne du cercle de rayon
fournit une équation
cartésienne du cercle de rayon ![]() et de centre
et de centre
![]() (6.8).
(6.8).
![]() est un paramétrage local de
est un paramétrage local de ![]() , alors en dérivant l'identité
, alors en dérivant l'identité
![]() , on obtient
, on obtient