



suivant: 6.4.3.2.3 Conclusions
monter: 6.4.3.2 Classification des courbes
précédent: 6.4.3.2.1 Les invariants
Table des matières
Comme la matrice  est symétrique, elle est diagonalisable (par une matrice orthogonale de déterminant
est symétrique, elle est diagonalisable (par une matrice orthogonale de déterminant 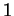 , si nécessaire) et ses valeurs propres sont réelles. On
peut donc choisir
, si nécessaire) et ses valeurs propres sont réelles. On
peut donc choisir  pour donner à (30) la forme
pour donner à (30) la forme
Deux remarques supplémentaires permettent de simplifier encore cette équation.
a)Si 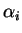 n'est pas nul, alors on peut faire en sorte que
n'est pas nul, alors on peut faire en sorte que 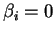 , et même que
, et même que
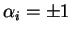 .
.
En effet, comme
(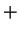 ou
ou 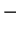 étant choisi selon que
étant choisi selon que 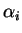 est positif ou négatif), il suffit de remplacer la coordonnée
est positif ou négatif), il suffit de remplacer la coordonnée 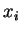 par
pour remplacer
par
pour remplacer 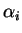 et
et 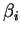 par
par 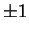 et 0 respectivement(6.14).
et 0 respectivement(6.14).
b)Si 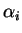 est nul et si
est nul et si 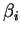 ne l'est pas, alors on peut supposer que
ne l'est pas, alors on peut supposer que 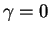 .
.
En effet, on peut alors changer 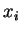 en
en
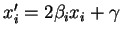 pour se débarrasser du terme indépendant.
pour se débarrasser du terme indépendant.




suivant: 6.4.3.2.3 Conclusions
monter: 6.4.3.2 Classification des courbes
précédent: 6.4.3.2.1 Les invariants
Table des matières
2002-12-17
![]() n'est pas nul, alors on peut faire en sorte que
n'est pas nul, alors on peut faire en sorte que ![]() , et même que
, et même que
![]() .
.
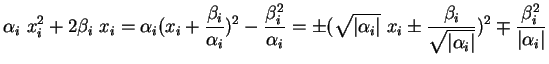
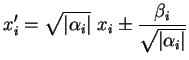
![]() est nul et si
est nul et si ![]() ne l'est pas, alors on peut supposer que
ne l'est pas, alors on peut supposer que ![]() .
.
![]() en
en
![]() pour se débarrasser du terme indépendant.
pour se débarrasser du terme indépendant.