



suivant: 7.5.2 La seconde forme
monter: 7.5.1 La première forme
précédent: 7.5.1.0.1 L'élément de longueur
Table des matières
Si l'on admet que, pour 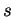 et
et 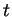 très petits, l'aire du parallélogramme de sommets
très petits, l'aire du parallélogramme de sommets  ,
,
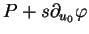 ,
,
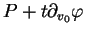 ,
,
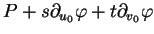 est une bonne approximation de l'aire de la surface
est une bonne approximation de l'aire de la surface
![$ \varphi(u,v), \
s\in[u_{0},u_{0}+s], \ t\in[v_{0},v_{0}+t]$](img2189.gif) , alors on peut aussi
comprendre que l'aire de la surface
, alors on peut aussi
comprendre que l'aire de la surface
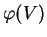 , où
, où
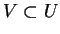 , est
donnée par
pour autant que cette intégrale existe.
Nous accepterons cette définition dont une justification plus complète
est du ressort de l'analyse(7.2).
, est
donnée par
pour autant que cette intégrale existe.
Nous accepterons cette définition dont une justification plus complète
est du ressort de l'analyse(7.2).
L'expression
est l'élément de surface de 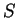 , exprimé dans le paramétrage
, exprimé dans le paramétrage
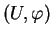 .
.
Proposition 7.5.4
L'élément de surface est donné par
Preuve. En effet, on a, en désignant par 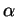 l'angle que font
l'angle que font
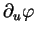 et
et
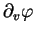 ,
D'où le résultat, vu l'expression de
,
D'où le résultat, vu l'expression de 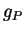 donnée plus haut.
donnée plus haut.
Voici la notion d'aire illustrée en géographie. La représentation plane de la surface de la Terre déforme
nécessairement les territoires représentés. La projection suivante
conserve les aires. Elle consiste à projeter un point de la sphère
terrestre perpendiculairement à l'axe des pôles sur le cylindre
circulaire droit contenant l'équateur et dont les génératrices
sont parallèles à cet axe. Le passage du cylindre au plan s'effectue
``en déroulant" le premier sur un de ses plans tangents. Le théorème suivant est attribué à Archimède!
Théorème 7.5.5
(Archimède)
La projection d'une sphère sur un cylindre circulaire
droit tangent à la sphère le long d'un grand cercle,
orthogonalement au diamètre perpendiculaire au plan de ce cercle
conserve les aires.
Preuve. Considérons la sphère et le cylindre tels qu'ils ont été
paramétrés dans les exemples (5.1) et (5.2).
Dans les paramétrages par les coordonnées sphériques et cylindriques,
l'élément de surface de la sphère est
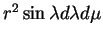 et celui du
cylindre est
et celui du
cylindre est 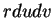 . De plus, l'expression de la projection considérée est
Elle fait donc correspondre le point de paramètres
. De plus, l'expression de la projection considérée est
Elle fait donc correspondre le point de paramètres
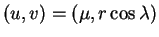 du
cylindre au point de paramètres
du
cylindre au point de paramètres
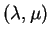 de la sphère. Le
Jacobien
de la sphère. Le
Jacobien 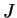 de ce changement de variables est
Si les ensembles
de ce changement de variables est
Si les ensembles
![$ V\subset ]0,\pi[\times ]0,2\pi[$](img2205.gif) et
et
![% latex2html id marker 36433
$ V'\subset]0,2\pi[\times {\rm I\!R}$](img2206.gif) se correspondent, l'aire de la portion
du cylindre paramétrée par
se correspondent, l'aire de la portion
du cylindre paramétrée par 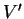 vaut, en application du théorème de
changement de variables dans les intégrales,
vaut, en application du théorème de
changement de variables dans les intégrales,
D'où le résultat car la dernière expression représente l'aire
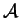 de la
portion de la sphère décrite par
de la
portion de la sphère décrite par 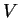 .
.
Pour justifier complètement l'utilisation du théorème d'Archimède,
il faut vérifier aussi qu'en ``déroulant" le cylindre dans un
de ses plans tangents, les aires sont également conservées. En
prenant le plan tangent en  de coordonnées
de coordonnées 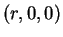 rapporté au
repère
rapporté au
repère
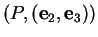 , le ``déroulement" fait correspondre le
point de coordonnées
, le ``déroulement" fait correspondre le
point de coordonnées 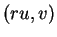 du plan au point de paramètres
du plan au point de paramètres  du cylindre(7.3). Les calculs peuvent alors être menés
comme dans la preuve précédente. Ils sont laissés à titre d'exercice.
du cylindre(7.3). Les calculs peuvent alors être menés
comme dans la preuve précédente. Ils sont laissés à titre d'exercice.




suivant: 7.5.2 La seconde forme
monter: 7.5.1 La première forme
précédent: 7.5.1.0.1 L'élément de longueur
Table des matières
2002-12-17
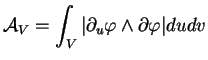
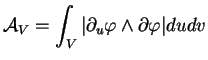
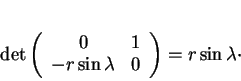
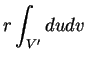
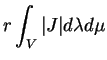
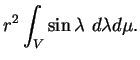
![]() de coordonnées
de coordonnées ![]() rapporté au
repère
rapporté au
repère
![]() , le ``déroulement" fait correspondre le
point de coordonnées
, le ``déroulement" fait correspondre le
point de coordonnées ![]() du plan au point de paramètres
du plan au point de paramètres ![]() du cylindre(7.3). Les calculs peuvent alors être menés
comme dans la preuve précédente. Ils sont laissés à titre d'exercice.
du cylindre(7.3). Les calculs peuvent alors être menés
comme dans la preuve précédente. Ils sont laissés à titre d'exercice.