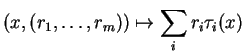- ... (1.1
- C'est-à-dire une bijection de classe
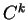 dont l'inverse est de classe
dont l'inverse est de classe 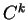 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
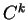 (1.2
(1.2
- Si on ne précise pas
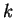 , on parle de variété différentielle
, on parle de variété différentielle
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (1.3
- Plus généralement,
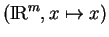 est la carte canonique de
est la carte canonique de
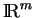 ; elle définit sa structure naturelle de variété plongée.
; elle définit sa structure naturelle de variété plongée.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.4
- Elles sont cependant difféomorphes (voir plus bas la définition de cette notion).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Lindelöf(1.5
- Tout recouvrement ouvert d'un espace topologique à base dénombrable, contient un recouvrement dénombrable
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.6
- Comme
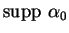 est compact,
est compact, 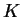 est compact car
est compact car
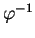 est continu.
est continu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.7
- Par algèbre on entend un espace vectoriel
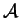 munit d'une application bilinéaire
munit d'une application bilinéaire
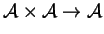 , la multiplication. Celle-ci est notée généralement par concaténation:
, la multiplication. Celle-ci est notée généralement par concaténation:
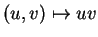 . Un isomorphisme d'algèbres est alors une bijection linéaire
. Un isomorphisme d'algèbres est alors une bijection linéaire
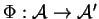 vérifiant
vérifiant
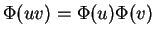 pour tous
pour tous
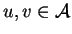 . Si les algèbres possèdent une unité - notée généralement
. Si les algèbres possèdent une unité - notée généralement 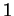 , on demande aussi que
, on demande aussi que 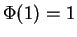
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.8
- Un idéal à gauche d'une algèbre
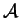 est un sous-espace vectoriel
est un sous-espace vectoriel 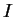 de
de
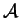 tel que
tel que
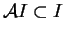 . On définit de façon similaire un idéal à droite. Lorsque
. On définit de façon similaire un idéal à droite. Lorsque
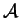 est commmutatif, les deux notions coïncident et on parle simplement d'idéaux.
est commmutatif, les deux notions coïncident et on parle simplement d'idéaux.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.9
- Par définition,
![$ f_0^{-1}([a,b])$](img314.gif) est compact pour tous
est compact pour tous
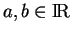 . Cette hypothèse n'est pas très contraignante mais nous ne saurions pas la discuter complètement ici. Par exemple, toutes les variétés plongées dans un espace euclidien y satisfont.
. Cette hypothèse n'est pas très contraignante mais nous ne saurions pas la discuter complètement ici. Par exemple, toutes les variétés plongées dans un espace euclidien y satisfont.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.10
- Du fait que
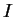 et les
et les 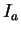 sont de même codimension, cela revient à supposer que, quelque soit
sont de même codimension, cela revient à supposer que, quelque soit 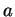 ,
,
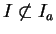 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(1.11
- Sinon, il serait égal à
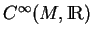 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... compact(1.12
- C'est un fermé, par continuité de
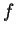 , contenu dans un compact.
, contenu dans un compact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.1
- Certains faits relatifs à la notion de dual sont rappelés au chapitre 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.2
- Dans cet énoncé,
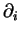 désigne la dérivée partielle par rapport à la coordonnée locale
désigne la dérivée partielle par rapport à la coordonnée locale 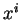 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.3
- Noter que
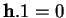 puisque
puisque
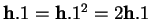 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.4
- L'expression
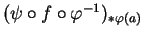 désigne la différentielle de
désigne la différentielle de
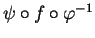 comme application entre ouverts d'espaces euclidiens, telle que définie dans des cours antérieurs. Elle coïncide avec celle d'application linéaire tangente si on identifie l'espace tangent à
comme application entre ouverts d'espaces euclidiens, telle que définie dans des cours antérieurs. Elle coïncide avec celle d'application linéaire tangente si on identifie l'espace tangent à
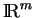 en chaque point à
en chaque point à
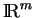 , conformément à la remarque 1.3.
, conformément à la remarque 1.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.5
- Un ouvert de
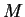 étant une union de cartes de
étant une union de cartes de 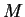 , celles-ci en définissent une structure de variété. C'est toujours de celle-là qu'il sera question à propos de la structure de variété des ouverts de
, celles-ci en définissent une structure de variété. C'est toujours de celle-là qu'il sera question à propos de la structure de variété des ouverts de 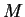
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.6
- Ceci appelle quelques remarques. D'abord, nous les noterons usuellement
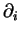 sauf s'il est nécessaire de faire référence aux coordonnées locales considérées. Ensuite,
sauf s'il est nécessaire de faire référence aux coordonnées locales considérées. Ensuite,
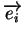 désigne le
désigne le 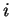 -ème vecteur de la base canonique de
-ème vecteur de la base canonique de
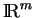 . Enfin, pour éviter une quelconque ambiguité, on précisera éventuellement le point en lequel
. Enfin, pour éviter une quelconque ambiguité, on précisera éventuellement le point en lequel
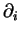 est tangent en notant plus précisément
est tangent en notant plus précisément
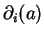 celui-ci.
celui-ci.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
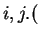 2.7
2.7
- Le plus souvent, on oubliera d'écrire le ``$.$'' et l'on notera $&part#partial;_ix^j$ ce qu'on devrait noter $&part#partial;_i.x^j$. Plus généralement, on se permettra à l'occasion d'écrire $&part#partial;_if$ à la place de $&part#partial;_i.f$.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.8
- Une submersion est une application
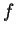 pour laquelle
pour laquelle 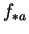 est surjectif en tout
est surjectif en tout 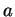 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (2.9
- La signification du mot fibré ne sera pas donnée à ce stade. Il faut prendre l'expression ``fibré tangent'' comme un tout insécable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.10
- Ainsi, la différentielle d'une application différentiable entre variétés est de nouveau une application différentiable entre variétés.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.11
- Si
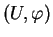 et
et 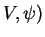 sont des cartes de variétés
sont des cartes de variétés 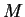 et
et 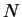 , alors
, alors
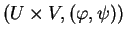 en est une de
en est une de 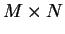 . Avec ces cartes,
. Avec ces cartes, 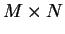 est muni d'une structure de variété, appelée produit cartésien des structures de
est muni d'une structure de variété, appelée produit cartésien des structures de 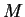 et de
et de 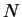 . Sauf mention explicite du contraire, c'est toujours cette structure dont nous munirons les produits
. Sauf mention explicite du contraire, c'est toujours cette structure dont nous munirons les produits 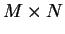 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.12
- Pour tout produit cartésien, nous noterons
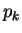 la projection sur le facteur de numéro
la projection sur le facteur de numéro 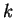 , pour autant qu'il n'en résulte aucune confusion.
, pour autant qu'il n'en résulte aucune confusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(2.13
- La réciproque est vraie: une parallélisation donne un difféomorphisme
entre
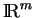 et
et 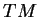 , linéaire sur les facteurs de droite.
, linéaire sur les facteurs de droite.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parallélisation(2.14
- Cet exemple généralise les deux précédents,
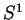 et
et 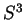 pouvant être considérés comme des sous-groupes de
pouvant être considérés comme des sous-groupes de
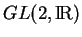 et
et
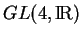 respectivement, un élément
respectivement, un élément 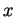 de ces sphères,
de ces sphères, 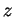 ou
ou 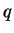 , étant confondu avec la multiplication à gauche
, étant confondu avec la multiplication à gauche
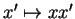 par
par 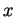 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
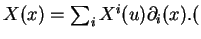 3.1
3.1
- Dans la suite, selon les circonstances, nous noterons $X(x)$ ou $X_x$ la valeur de $X$ en $x&isin#in;M$.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lui-même(3.2
- C'est la restriction à
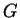 d'une application de classe
d'une application de classe 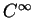 de
de
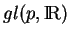 dans lui-même, à savoir
dans lui-même, à savoir
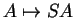 . Un lemme analogue au précédent permettrait de conclure. Nous ne détaillerons pas.
. Un lemme analogue au précédent permettrait de conclure. Nous ne détaillerons pas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... forme(3.3
- Cela ne sera pas vérifié explicitement ici.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(3.4
- En fait, on peut vérifier que si
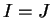 , alors
, alors 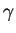 et
et 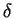 sont automatiquement égaux.
sont automatiquement égaux.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complets(3.5
- Plus généralement, les champs de vecteurs à support compact sont toujours complets.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sait(3.6
- Ceci sera redémontré plus bas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(3.7
- La proposition 2.3 étant vraie également en classe
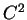 , on pourrait améliorer cette hypothèse.
, on pourrait améliorer cette hypothèse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... entier(3.8
- En fait
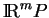 est compact. Ses champs de vecteurs sont donc tous complets.
est compact. Ses champs de vecteurs sont donc tous complets.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (3.9
- Les applications
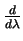 et
et
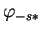 commutent car celle-ci est une application entre espaces vectoriels de dimension finie. La vérification est aisée en passant à des bases.
commutent car celle-ci est une application entre espaces vectoriels de dimension finie. La vérification est aisée en passant à des bases.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
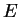 (4.1
(4.1
- En particulier, les dimensions de
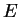 et de
et de 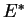 sont égales.
sont égales.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... duales(4.2
- L'indice supérieur est celui décrivant les lignes de la matrice.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.1
- Ayant utilisé
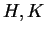 pour désigner des champs de vecteurs sur
pour désigner des champs de vecteurs sur 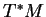 , nous utiliserons
, nous utiliserons
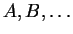 pour désigner des vecteurs tangents à
pour désigner des vecteurs tangents à 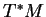 ...
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inverse(5.2
- ... et nous utiliserons
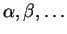 pour désigner des vecteurs cotangents à
pour désigner des vecteurs cotangents à 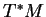 afin de les distinguer de ceux qui sont cotangents à
afin de les distinguer de ceux qui sont cotangents à 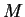 et que nous avons notés
et que nous avons notés
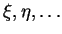
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.3
- Il serait un peu lourd d'écrire
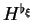 Aussi, nous ne rapellerons généralement pas
Aussi, nous ne rapellerons généralement pas 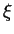 en indice de
en indice de 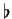 . Remarque analogue pour
. Remarque analogue pour 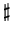 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... entier(5.4
- Relire leurs démonstrations pour s'en convaincre
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![$ \oint_{HKL}H.\omega^M_\xi(K,L)=\oint_{HKL}\omega^M_\xi([H,K],L)($](img1089.gif) 5.5
5.5
- Le symbole $&conint#oint;_abc$ représente la somme sur les permutations circulaires de $a,b,c$
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(5.6
- ou sur un domaine
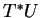 de carte canonique, la question étant manifestement locale.
de carte canonique, la question étant manifestement locale.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... canoniques(5.7
- Voir la démonstration de la proposition 2.1 pour se rappeler l'expression locale de
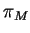 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formel(5.8
- Dans le langage général des formes difféentielles, la première relation signifie que la forme symplectique est fermée. La seconde signifie qu'elle est exacte. Il se fait que toute forme exacte est automatiquement fermée, la réciproque n'étant pas toujours vraie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... classique(6.1
- Ici les contraintes sont indépendante s du temps. Il faudrait introduire une structure de contact - ajouter une dimension - pour tenir compte de contraintes non autonomes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... démonstration(6.2
- Elle n'est pas vraie sur toutes les variétés symplectiques. Par exemple, elle est fausse sur les variétés symplectiques compactes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polynômes(6.3
- La caractérisation à laquelle nous parviendrons se transpose en fait à tout les fibrés vectoriels. Elle s'applique par exemple ainsi au fibré tangent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... que(6.4
- D'après a),
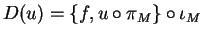 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.