


suivant: 1.3.0.0.1 Avertissement
monter: 1 Variétés différentielles
précédent: 1.2.0.0.1 Avertissement
Table des matières
Soient des variétés différentielles  et
et 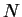 , de classe
, de classe 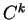 . Une application
. Une application 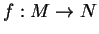 est de classe
est de classe 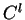 , avec
, avec
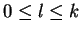 , si, pour tout
, si, pour tout 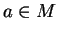 , il existe des cartes
, il existe des cartes
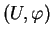 de
de  et
et 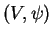 de
de  telles que
telles que 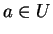 ,
,
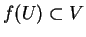 et
soit de classe
et
soit de classe 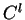 . Cette application s'appelle l'expression locale de
. Cette application s'appelle l'expression locale de 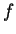 dans les cartes
dans les cartes
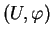 et
et 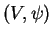 .
.
Il est utile d'observer que
Remarque 1.3.1
Si
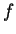
est de classe
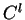
, alors ses expressions locales dans toutes cartes
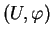
et
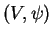
telles que
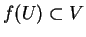
sont de classe
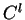
.
En effet, soient
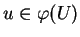 ,
,
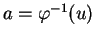 et des cartes
et des cartes
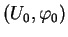 et
et
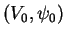 dans lesquelles l'expression locale de
dans lesquelles l'expression locale de 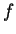 est de classe
est de classe 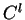 , avec
, avec 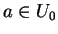 . Il suffit de noter que
. Il suffit de noter que
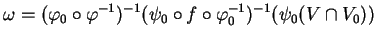 |
(1.1) |
est un ouvert de
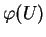 , contenant
, contenant 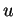 , et que, dans celui-ci,
ce qui prouve que
, et que, dans celui-ci,
ce qui prouve que
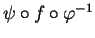 est de classe
est de classe 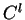 au voisinage de
au voisinage de 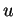 puisque les changements de cartes
puisque les changements de cartes
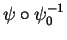 et
et
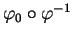 sont des difféomorphismes de classe
sont des difféomorphismes de classe 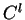 . En ce qui concerne (1), on remarque que
. En ce qui concerne (1), on remarque que
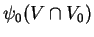 est ouvert par définition de la compatibilité des cartes, ensuite on conclut en utilisant le fait que
est ouvert par définition de la compatibilité des cartes, ensuite on conclut en utilisant le fait que
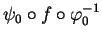 et
et
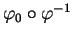 sont continus.
sont continus.
Chemin faisant, nous venons de voir que
Remarque 1.3.2
Si
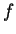
est de classe
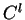
et si les domaines des cartes
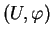
et
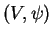
contiennent

et
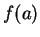
respectivement, alors on peut restreindre
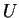
pour qu'en outre
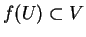
.
En particulier, les fonctions de classe 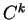 entre variétés sont continues.
Nous utiliserons ce fait librement dans la suite, de même que le suivant.
entre variétés sont continues.
Nous utiliserons ce fait librement dans la suite, de même que le suivant.
Remarque 1.3.3
Soit une carte
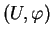
. Si le support de
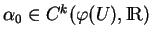
est compact, alors
appartient à
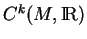
.
Figure 1:
Allure de 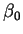 .
.
|
|
Voici comment on peut vérifier ceci.
Soit 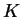 le compact
le compact
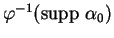 de
de 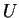 (1.6).
Soit
(1.6).
Soit 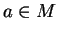 . Nous devons vérifier qu'il existe une carte de
. Nous devons vérifier qu'il existe une carte de  dont le domaine contient
dont le domaine contient  et dans laquelle l'expression locale de
et dans laquelle l'expression locale de 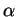 est de classe
est de classe 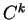 .
Si
.
Si 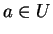 , on peut prendre
, on peut prendre
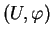 , dans laquelle cette expression locale est
, dans laquelle cette expression locale est 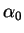 .
Si
.
Si 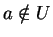 , alors
, alors 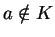 . Comme
. Comme 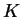 est compact, il est fermé (puisque la topologie de
est compact, il est fermé (puisque la topologie de  est séparée). Son complémentaire est donc ouvert: il existe une carte
est séparée). Son complémentaire est donc ouvert: il existe une carte 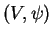 dont le domaine contient
dont le domaine contient  et est disjoint de
et est disjoint de 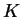 . L'expression locale de
. L'expression locale de 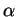 dans cette carte est nulle.
dans cette carte est nulle.
Avec la remarque précédente, on construit facilement des fonctions ayant un comportement prescrit en  . En effet, En prenant
. En effet, En prenant 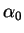 de la forme
de la forme 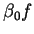 où
où 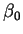 est à support compact dans
est à support compact dans
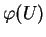 , est à valeurs dans
, est à valeurs dans ![$ [0,1]$](img146.gif) et vaut
et vaut 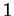 dans un voisinage de
dans un voisinage de
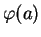 , on obtient une fonction
, on obtient une fonction 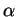 dont l'expression locale coincide avec
dont l'expression locale coincide avec
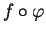 au voisinage de
au voisinage de  .
.
Si 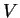 est une variété plongée dans
est une variété plongée dans
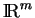 , de classe
, de classe 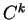 , alors l'identité
, alors l'identité
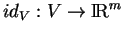 est une application de classe
est une application de classe 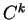 . En effet, pour tout paramétrage
. En effet, pour tout paramétrage
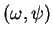 de
de 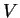 , l'expression locale de
, l'expression locale de 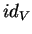 dans les cartes
dans les cartes
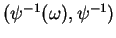 et
et
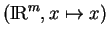 est
est 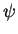 , qui est de classe
, qui est de classe 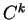 par hypothèse.
par hypothèse.
Une application linéaire 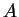 non singulière de
non singulière de
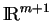 dans lui-même induit une bijection
dans lui-même induit une bijection 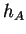 de
de
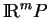 dans lui-même. Elle transforme la droite
dans lui-même. Elle transforme la droite 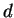 de vecteur directeur
de vecteur directeur 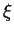 en
en
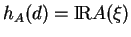 . Elle est de classe
. Elle est de classe  . Utilisons pour vérifier cela les cartes introduites dans l'exemple 1.1. En supposant, pour simplifier les notations, que
. Utilisons pour vérifier cela les cartes introduites dans l'exemple 1.1. En supposant, pour simplifier les notations, que
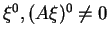 , l'expression locale
, l'expression locale
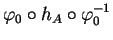 de
de 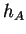 dans la carte
dans la carte
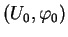 est
Cette application n'étant définie que dans le complémentaire
est
Cette application n'étant définie que dans le complémentaire 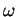 de l'hyperplan d'équation
de l'hyperplan d'équation
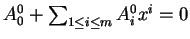 , il faut, pour ce conformer à la définition des applications différentiables, restreindre le domaine de la carte
, il faut, pour ce conformer à la définition des applications différentiables, restreindre le domaine de la carte
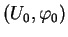 à
à
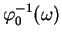 .
.
Proposition 1.3.6
Si les applications
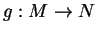
et
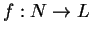
sont de classe
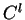
, alors
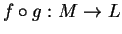
est de classe
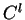
.
Preuve.
Soient
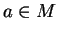
,
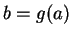
et des cartes
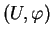
,
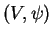
et
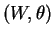
telles que
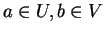
et
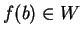
. Quitte à restreindre
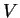
d'abord,
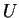
ensuite, nous pouvons supposer que
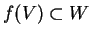
puis
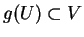
. L'expression locale de
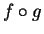
dans les cartes
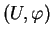
et
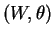
se factorise alors en applications de classe
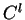
:
Elle est donc de classe
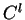
.
Nous noterons 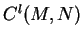 l'ensemble des applications de classe
l'ensemble des applications de classe 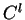 de
de  dans
dans 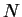 .
Lorsque
.
Lorsque
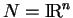 , c'est un espace vectoriel sur
, c'est un espace vectoriel sur
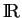 , les opérations vectorielles étant définies point par point. Lorsque
, les opérations vectorielles étant définies point par point. Lorsque
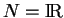 , c'est même une algèbre, la multiplication étant définie également ponctuellement.
, c'est même une algèbre, la multiplication étant définie également ponctuellement.
Nous appellerons courbe de  (de classe
(de classe 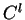 si il faut le préciser) les éléments de
si il faut le préciser) les éléments de 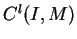 , où
, où 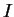 est un intervalle ouvert de
est un intervalle ouvert de
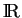 .
.
Une bijection 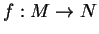 est un difféomorphisme de classe
est un difféomorphisme de classe 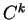 si
si 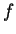 et
et 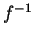 sont de classe
sont de classe 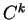 . Si
. Si
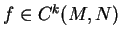 est un difféomorphisme, alors il transforme les cartes
est un difféomorphisme, alors il transforme les cartes
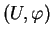 de
de  en des cartes
en des cartes
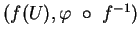 de
de  . De plus, toutes les cartes de
. De plus, toutes les cartes de  sont de cette forme. De ce fait, on considère généralement que, du point de vue de la géométrie différentielle, des variétés difféomorphes sont égales.
sont de cette forme. De ce fait, on considère généralement que, du point de vue de la géométrie différentielle, des variétés difféomorphes sont égales.
Sous-sections



suivant: 1.3.0.0.1 Avertissement
monter: 1 Variétés différentielles
précédent: 1.2.0.0.1 Avertissement
Table des matières
2003-11-02
![]() le compact
le compact
![]() de
de ![]() (1.6).
Soit
(1.6).
Soit ![]() . Nous devons vérifier qu'il existe une carte de
. Nous devons vérifier qu'il existe une carte de ![]() dont le domaine contient
dont le domaine contient ![]() et dans laquelle l'expression locale de
et dans laquelle l'expression locale de ![]() est de classe
est de classe ![]() .
Si
.
Si ![]() , on peut prendre
, on peut prendre
![]() , dans laquelle cette expression locale est
, dans laquelle cette expression locale est ![]() .
Si
.
Si ![]() , alors
, alors ![]() . Comme
. Comme ![]() est compact, il est fermé (puisque la topologie de
est compact, il est fermé (puisque la topologie de ![]() est séparée). Son complémentaire est donc ouvert: il existe une carte
est séparée). Son complémentaire est donc ouvert: il existe une carte ![]() dont le domaine contient
dont le domaine contient ![]() et est disjoint de
et est disjoint de ![]() . L'expression locale de
. L'expression locale de ![]() dans cette carte est nulle.
dans cette carte est nulle.
![]() . En effet, En prenant
. En effet, En prenant ![]() de la forme
de la forme ![]() où
où ![]() est à support compact dans
est à support compact dans
![]() , est à valeurs dans
, est à valeurs dans ![]() et vaut
et vaut ![]() dans un voisinage de
dans un voisinage de
![]() , on obtient une fonction
, on obtient une fonction ![]() dont l'expression locale coincide avec
dont l'expression locale coincide avec
![]() au voisinage de
au voisinage de ![]() .
.
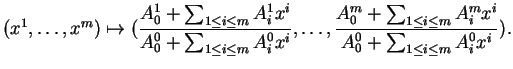
![]() l'ensemble des applications de classe
l'ensemble des applications de classe ![]() de
de ![]() dans
dans ![]() .
Lorsque
.
Lorsque
![]() , c'est un espace vectoriel sur
, c'est un espace vectoriel sur
![]() , les opérations vectorielles étant définies point par point. Lorsque
, les opérations vectorielles étant définies point par point. Lorsque
![]() , c'est même une algèbre, la multiplication étant définie également ponctuellement.
, c'est même une algèbre, la multiplication étant définie également ponctuellement.
![]() (de classe
(de classe ![]() si il faut le préciser) les éléments de
si il faut le préciser) les éléments de ![]() , où
, où ![]() est un intervalle ouvert de
est un intervalle ouvert de
![]() .
.
![]() est un difféomorphisme de classe
est un difféomorphisme de classe ![]() si
si ![]() et
et ![]() sont de classe
sont de classe ![]() . Si
. Si
![]() est un difféomorphisme, alors il transforme les cartes
est un difféomorphisme, alors il transforme les cartes
![]() de
de ![]() en des cartes
en des cartes
![]() de
de ![]() . De plus, toutes les cartes de
. De plus, toutes les cartes de ![]() sont de cette forme. De ce fait, on considère généralement que, du point de vue de la géométrie différentielle, des variétés difféomorphes sont égales.
sont de cette forme. De ce fait, on considère généralement que, du point de vue de la géométrie différentielle, des variétés difféomorphes sont égales.