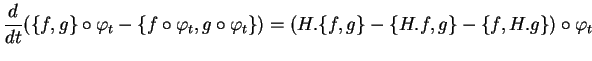


suivant: 6.4 Les observables classiques
monter: 6 L'algèbre de Poisson
précédent: Intégrales premières des équations
Table des matières
D'après l'identité de Jacobi pour le crochet de Poisson, les champs hamiltoniens sont des champs 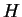 vérifiant l'égalité
vérifiant l'égalité
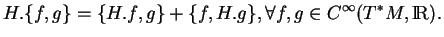 |
(6.1) |
Un champ de vecteurs 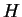 ayant cette propriété est dit symplectique.
ayant cette propriété est dit symplectique.
Proposition 6.3.1
Un champ de vecteurs
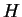
de
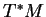
est symplectique si et seulement si tout point de
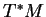
appartient à un ouvert dans lequel il coïncide avec un champ hamiltonien.
Preuve.
Exprimons la condition (
19) en coordonnées canoniques.
Notons
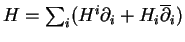
l'expression locale de
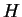
. En prenant successivement pour
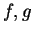
les fonctions
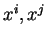
, puis
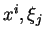
et
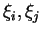
, on obtient les équations
Quitte à rétrécir
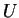
, on peut donc trouver une primitive
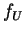
aux fonctions
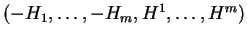
, ce qui signifie que, dans
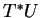
, le champ
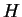
coïncide avec le champ hamiltonien
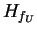
.
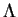
Proposition 6.3.2
Le crochet de Lie de champs symplectiques est un champ hamiltonien. En particulier, l'ensemble des champs symplectiques est une sous-algèbre de Lie de
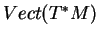
.
Preuve.
Soient des champs symplectiques
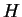
et
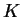
. On a vu dans le preuve précédente que si le domaine
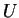
d'une carte de
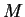
est assez petit, alors il existe des fonctions
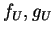
de classe
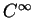
dans
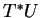
dont
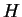
et
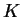
soient les champs hamiltoniens dans cet ouvert. Il est clair que ces fonctions sont localement déterminées à des constantes près. Il en résulte qu'il existe une fonction
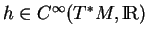
telle que
quel que soit le domaine de carte
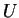
ayant les propriétés ci-dessus.
On a
![$ [H,K]=H_h$](img1182.gif)
.
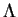
Proposition 6.3.3
Soient un champ de vecteurs
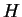
de
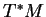
et
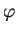
son flot. Le champ
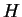
est symplectique si et seulement si
pour tout
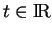
et tous
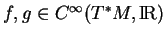
.
Preuve.
Quitte à passer à des coordonnées pour effectuer les calculs, on peut vérifier que
Le fait que
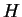
soit symplectique équivaut donc au fait que
est constant, c'est-à-dire nul puisqu'il s'annule en
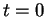
.
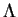
Les champs symplectiques génèrent donc des flots d'automorphismes (locaux) de l'algèbre de Poisson.
Concluons cette section par la proposition suivante que nous admettrons sans démonstration(6.2).
Proposition 6.3.4
Une application linéaire
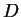
est une dérivation de l'algèbre de Lie de Poisson si et seulement si il existe un champ symplectique
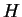
tel que
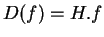
pour tout
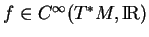
.



suivant: 6.4 Les observables classiques
monter: 6 L'algèbre de Poisson
précédent: Intégrales premières des équations
Table des matières
2003-11-02
![]() ayant cette propriété est dit symplectique.
ayant cette propriété est dit symplectique.
![\begin{displaymath}
% latex2html id marker 14918\left\{
\begin{array}{rcl}
\ov...
...H_j\\ [1ex]
\partial_iH_j&=&\partial_jH_i.
\end{array}\right.
\end{displaymath}](img1174.gif)