


suivant: Le champ d'Euler
monter: 6 L'algèbre de Poisson
précédent: 6.3 Les champs symplectiques
Table des matières
On appelle parfois les fonctions sur l'espace de phases les observables classiques, classiques par oppositions aux observables quantiques qui sont généralement d'une autre nature mathématique. Dans les deux cas, mécanique classique ou quantique, il s'agit des notions mathématiques modélisant les grandeurs physiques associées à un système mécanique: énergie, position, impulsion, moments, ...
Le hamiltonien d'un système est par exemple l'observable mesurant son énergie. La composante cinétique de celle-ci est quadratique en les vitesses - ou encore en les impulsions. Plus généralement, les observables classiques sont souvent polynômiales en les variables 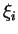 représentant les impulsions.
représentant les impulsions.
Nous allons voir comment on peut caractériser les fonctions sur 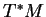 dont les restrictions aux espaces vectoriels
dont les restrictions aux espaces vectoriels 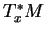 ,
, 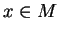 , sont des polynômes(6.3).
, sont des polynômes(6.3).
Sous-sections
2003-11-02
![]() représentant les impulsions.
représentant les impulsions.
![]() dont les restrictions aux espaces vectoriels
dont les restrictions aux espaces vectoriels ![]() ,
, ![]() , sont des polynômes(6.3).
, sont des polynômes(6.3).