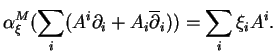Preuve.
En coordonnées canoniques,
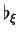
est donné par l'application linéaire
Par conséquent,
ce qui démontre que
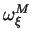
est antisymétrique et non dégénéré. En outre, nous constatons que
ses coefficients sont constants puisque la matrice représentant cette forme dans la base des
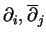
est
Voici comment nous allons faire pour vérifier l'identité (
15). Posons d'abord, pour alléger les écritures,
Nous allons alors montrer que pour toute fonction
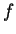
de classe
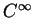
sur
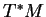
(
5.6), à valeurs dans
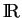
,
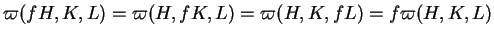 |
(5.5) |
quels que soient
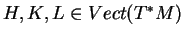
. En développant les champs de vecteurs
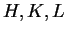
selon la base locale des
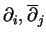
associée à une carte canonique, il en résulte que
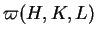
est, dans
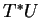
, une combinaison linéaire des fonctions
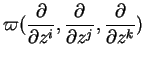 |
(5.6) |
où nous avons posé
Nous montrerons que ces fonctions sont nulles, prouvant ainsi (
15).
En fait, (16) résulte facilement d'un calcul direct utilisant l'identité 1.3.
Par ailleurs, pour s'assurer de ce que (17) est nul, on note que les champs
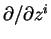 commutent deux à deux et que les coefficents
commutent deux à deux et que les coefficents
sont constants.
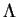
Preuve.
La démonstration est analogue à celle que nous avons appliquée à (
15). On pose
Un calcul direct ne présentant aucune difficulté montre que
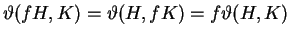
pour tout
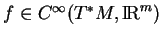
. On est donc ramené à établir (
18) lorsque
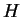
et
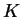
décrivent les éléments d'une base locale associée à des coordonnées canoniques, ce qui est immédiat (ne pas oublier que ces champs commutent deux à deux). Par exemple
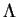
![$\displaystyle \oint_{HKL}H.\omega^M_\xi(K,L)=\oint_{HKL}\omega^M_\xi([H,K],L)(\footnotemark ).$](img1090.gif)
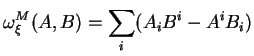
![$\displaystyle \varpi_\xi(H,K,L)=\oint_{HKL}\{H_\xi.\omega^M(K,L)-\omega^M_\xi([H,K],L)\}.
$](img1095.gif)
![]() commutent deux à deux et que les coefficents
commutent deux à deux et que les coefficents
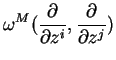
![]() -forme particulière de
-forme particulière de ![]() , la forme de Liouville
, la forme de Liouville ![]() . Celle-ci est défnie par
. Celle-ci est défnie par