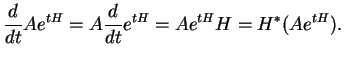| (3.3) |
En coordonnées locales, la condition (9) se traduit par un système d'équations différentielles ordinaires autonomes. De fait, si ![]() est l'expression locale
est l'expression locale
![]() de
de ![]() dans une carte
dans une carte
![]() , alors
, alors
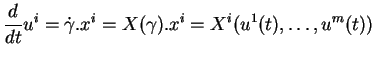
Les propriétés des courbes intégrales d'un champs de vecteurs se déduisent alors de celles des solutions d'un tel système. Nous n'entrerons pas dans les détails. Signalons cependant les faits suivants qui en résultent facilement, avant d'étudier plus avant les courbes maximales. Notons aussi que le fait que la topologie de ![]() est séparée est important pour les résultats énoncés ci-dessous.
est séparée est important pour les résultats énoncés ci-dessous.
Ces deux propriétés permmettent de vérifier que pour tout ![]() ,
, ![]() possède une unique courbe intégrale maximale passant par
possède une unique courbe intégrale maximale passant par ![]() en
en ![]() . On la note
. On la note
![]() et, pour
et, pour ![]() fixé, on désigne par
fixé, on désigne par ![]() l'ensemble des
l'ensemble des ![]() pour lesquels
pour lesquels
![]() . Nous acceptons la proposition suivante sans démonstration.
. Nous acceptons la proposition suivante sans démonstration.
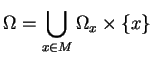
L'application
![]() s'appelle le flot de
s'appelle le flot de ![]() . Quand son domaine de définition est
. Quand son domaine de définition est
![]() tout entier, on dit de
tout entier, on dit de ![]() que c'est un champ de vecteurs complet.
On peut montrer que si
que c'est un champ de vecteurs complet.
On peut montrer que si ![]() est compact, alors tous ses champs de vecteurs sont complets(3.5).
est compact, alors tous ses champs de vecteurs sont complets(3.5).
Le flot du champ
![]() est l'application
est l'application