2.3 Quelques remarques en vrac

Voici quelques remarques qui résultent plus ou moins immédiatement des définitions et résultats précédent.

Remarque 2.3.1   Si ${\bf h}=\dot{\gamma}(s)$ alors $f_{*a}{\bf h}$ est le vecteur tangent en $s$ à la courbe $f\circ\gamma$ de $N$.

En effet,

$$f_{*a}{\bf h}.g={\bf h}.(g\circ f)={... ...d}{dt}{((g\circ f)\circ\gamma)}}(s)={\frac{d}{dt}{(g\circ(f\circ\gamma))}}(s).$$

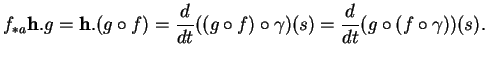
De là, il résulte que

Remarque 2.3.2   si $(U,\varphi)$ et $(V,\psi)$ sont des cartes de $M$ et de $N$ telles que $a\in U$ et $f(U)\subset V$, alors l'expression locale de $f_{*a}$ est $(\psi\circ f\circ\varphi^{-1})_{*\varphi(a)}$(^2.4).

En effet, on a vu plus haut que les composantes de l'expression locale de ${\bf h}=\dot{\gamma(s)}$ dans la carte $(U,\varphi)$ sont les $h^i={\frac{d}{dt}{(\varphi^i\circ\gamma)}}(s)$. Celles de l'expression locale de $f_{*a}{\bf h}$ dans la carte $(V,\psi)$ sont donc les composantes de la dérivée de $\psi\circ (f\circ\gamma)=(\psi\circ f\circ \varphi^{-1})\circ(\varphi\circ\gamma)$ en $t=s$. Il s'agit donc bien de la dérivée de $\psi\circ f\circ\varphi^{-1}$ dans la direction de $(h^1,\ldots,h^m)$.

Remarque 2.3.3   Espace tangent aux variétés plongées.

Nous avons observé plus haut qu'une variété $V$ plongée dans ${\rm I\!R}^m$ est également une variété au sens abstrait introduit dans ces notes. Nous avons en particulier vu, dans l'exemple , que l'identité $i_V:V\to{\rm I\!R}^m$ est de même classe que $V$. Par conséquent, si ${\bf h}=\dot{\gamma}(s)\in T_aV$, alors ${i_V}_{*a}{\bf h}$ est le vecteur tangent à la courbe $i_V\circ\gamma=\gamma$ de ${\rm I\!R}^m$ lequel est, par définition, un élément de $\overrightarrow{T_aV}$. On a donc ${i_V}_{*a}T_aV=\overrightarrow{T_aV}$. Les dimensions de $T_aV$ et de $\overrightarrow{T_aV}$ étant égales, il en résulte que ${i_V}_{*a}$ est effectivement une bijection.

Remarque 2.3.4   Vecteurs tangents et fonctions définies dans un ouverts.

Soit ${\bf h}\in T_aM$. Si deux fonctions $f$ et $f'$ coïncident dans un ouvert contenant $a$, alors il résulte immédiatement de la formule (4) du théorème 1.1 que ${\bf h}.f={\bf h}.f'$. On peut donc étendre ${\bf h}$ aux fonctions qui sont de classe $C^\infty$ dans un ouvert $\omega$ de $M$ contenant $a$ en posant, pour tout $f\in C^\infty(\omega,{\rm I\!R})$, ${\bf h}.f={\bf h}.\hat{f}$, où la fonction $\hat{f}$ de classe $C^\infty$ dans $M$ coïncide avec $f$ dans un voisinage de $a$. En particulier, considérant $\omega$ muni de la structure de variété dont il hérite de $M$(^2.5), on écrira en conséquence $T_a\omega=T_aM$. Nous utiliserons librement cette égalité dans la suite.

Remarque 2.3.5   Si $(U,\varphi)$ est une carte de $M$, alors $\varphi:U\to\varphi(U)$ est un difféomorphisme et son application linéaire tangente en $a\in U$ coïncide avec l'application notée $\varphi_{*a}$ au point c) du théorème 1.1.

C'est immédiat.

Remarque 2.3.6   Si $(U,\varphi)$ est une carte de $M$, alors les vecteurs

$$\frac{\partial}{\partial x^i} =\varphi_{*a}^{-1}\overrightarrow{e_i},\ i=1,\ldots,m,$$

constituent une base de $T_aM$ en tout point $a$ de $U$(^2.6). En particulier, si l'expression locale de ${\bf h}\in T_aM$ est $(h^1,\ldots,h^m)$, alors on peut écrire

$${\bf h}=\sum_ih^i\partial_i.$$

Par exemple, si $M$ est une variété plongée dans ${\rm I\!R}^m$ et si $(\omega,\psi)$ en est un paramétrage, les champs $\partial_i$ associés à la carte $(U=\psi(\omega),\varphi=\psi^{-1})$ sont les champs $\partial_1\psi,\ldots,\partial_p\psi$.

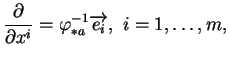
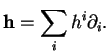
On a déjà observé que $h^i={\bf h}.x^i$, où $x^i$ désigne la $i$-ème coordonnée locale. La notation ci-dessus est en parfait accord avec cela puisque tout se passe formellement comme si les applications $x^j:U\to{\rm I\!R}$ et $\partial_j: C^\infty(M,{\rm I\!R})\to{\rm I\!R}$ représentaient les variables ordinaires dans ${\rm I\!R}^m$ et les dérivéees partielles par rapport à celles-ci. En effet, à l'instar de ces dernières, ces applications vérifient les égalités

$$\partial_i.x^j=\delta_i^j, \ \forall i,j.(\footnotemark )$$

Dans ${\rm I\!R}^m$ rapporté à la carte canonique $({\rm I\!R}^m,id)$, on a $\partial_i=\overrightarrow{e_i}$.