Une dérivation de
![]() est une application linéaire
est une application linéaire
![]() telle que
telle que
i)Pour chaque ![]() ,
, ![]() est une dérivation. La fonction
est une dérivation. La fonction ![]() est de classe
est de classe ![]() car, dans toute carte
car, dans toute carte
![]() de
de ![]() , on a, d'après (4),
, on a, d'après (4),
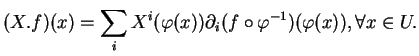
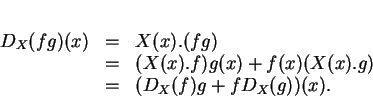
ii)L'application
![]() est injective. Si
est injective. Si ![]() , alors
, alors ![]() pour tout
pour tout ![]() . Dès lors, étant donné
. Dès lors, étant donné ![]() ,
,
![]() pour tout
pour tout ![]() . Les
. Les ![]() -dérivations
-dérivations ![]() et
et ![]() sont ainsi égales pour tout
sont ainsi égales pour tout ![]() . Donc
. Donc ![]() .
.
iii)L'application
![]() est surjective. Soit une dérivation
est surjective. Soit une dérivation ![]() de
de
![]() . Pour chaque
. Pour chaque ![]() , on obtient un vecteur tangent
, on obtient un vecteur tangent
![]() en posant
en posant
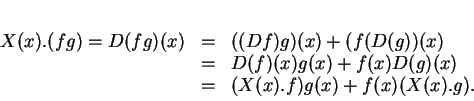
Le théorème précédent nous donne l'essentiel des propriétés de ![]() : c'est une algèbre de Lie, dont le crochet de Lie est défini par le commutateur d'applications linéaires. Voici résumées les principales opérations ainsi définies sur
: c'est une algèbre de Lie, dont le crochet de Lie est défini par le commutateur d'applications linéaires. Voici résumées les principales opérations ainsi définies sur ![]() .
.
Les composantes de ![]() dans une carte s'expriment au moyen de celles de
dans une carte s'expriment au moyen de celles de ![]() et de
et de ![]() par la formule
par la formule
![\begin{displaymath}
% latex2html id marker 12741\begin{array}{rcl}
[X,Y]^i&=&[...
... [1ex]
&=&\sum_j(X^j\partial Y^i-Y^j\partial X^i),
\end{array}\end{displaymath}](img647.gif)
En utilisant par exemple l'expression locale de ![]() , on voit immédiatement que
, on voit immédiatement que
Nous verifierons plus loin que pour les champs invariants à gauche d'un groupe,