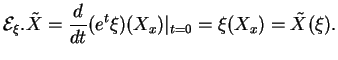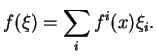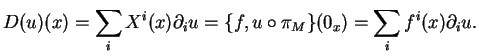Preuve.
Plaçons nous en coordonnées canoniques et identifions les éléments propres de
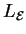
dans le domaine
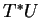
de celles-ci. Dans la mesure où les coordonnées
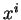
jouent un rôle secondaire dans le problème, l'expression locale
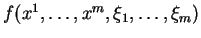
d'une fonction
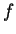
sera abrégée en
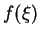
pour alléger les notations.
La condition pour que
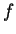
soit un vecteur propre de valeur propre
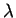
de
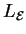
est
a) Ceci permet déjà de voir que les polynômes homogènes de degré
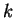
en les
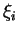
sont des vecteurs propres de valeur propre
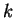
. En effet, pour un tel polynôme
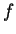
on a
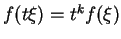
de sorte que
b) Supposons que f soit un vecteur propre de valeur propre
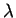
. On a alors
On a aussi
Au total,
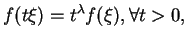 |
(6.2) |
car les deux membres sont tous deux solutions de l'équation différentielle
Cela étant si 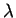 est un entier positif ou nul
est un entier positif ou nul 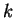 , alors en dérivant (20)
, alors en dérivant (20) 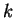 fois par rapport à
fois par rapport à 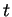 puis en passant à la limite en
puis en passant à la limite en 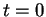 , on obtient
, on obtient
ce qui montre que
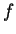
est bien un polynôme homogène de degré
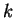
.
Par contre, lorsque
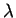
n'est pas un entier positif ou nul alors
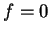
car si
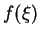
n'était pas nul, les dérivées de tout ordre de
par rapport à
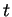
admettraient une limite lorsque
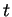
tend vers 0 par valeurs positives, ce qui n'est pas le cas.
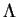
Preuve.
a) On a
car
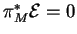
comme on le voit facilement avec la définition de
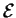
.
Donc
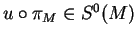
.
D'autre part, si
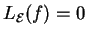
, alors
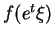
ne dépend pas de
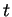
. Donc
où
b) Pour tout
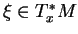
, on a
Donc
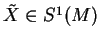
.
Inversement, supposons que
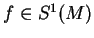
, alors, pour tout
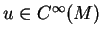
,
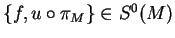
. Il existe donc une application linéaire
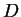
de
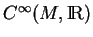
dans lui-même telle que(
6.4)
En appliquant d) de la proprosition
2.1, on voit que
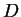
est une dérivation de
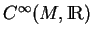
. On a donc
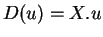
pour un certain champ de vecteurs
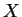
de

. Passons en coordonnées canoniques. Puisque
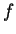
est un polynôme du premier degré, il s'écrit
Dès lors,
Comme
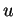
est arbitraire, on en déduit que
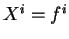
pour tout
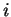
et donc que
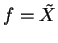
.
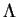
![]() est un polynôme de degré
est un polynôme de degré ![]() si ses restrictions aux espaces vectoriels
si ses restrictions aux espaces vectoriels ![]() ,
, ![]() , sont des polynômes de degré
, sont des polynômes de degré ![]() . Nous noterons
. Nous noterons ![]() l'espace de celles qui sont homogènes de degré
l'espace de celles qui sont homogènes de degré ![]() . L'espace des polynômes sur
. L'espace des polynômes sur ![]() est alors
est alors
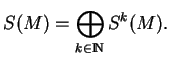
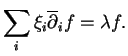
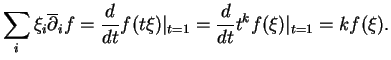
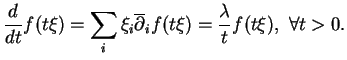
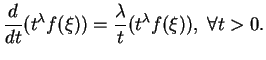
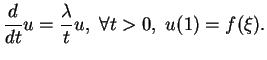
![]() est un entier positif ou nul
est un entier positif ou nul ![]() , alors en dérivant (20)
, alors en dérivant (20) ![]() fois par rapport à
fois par rapport à ![]() puis en passant à la limite en
puis en passant à la limite en ![]() , on obtient
, on obtient
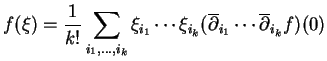
![]() de
de
![]() .
Dans la démonstration, on utilise la notation
.
Dans la démonstration, on utilise la notation ![]() . Celle-ci désigne la section nulle de
. Celle-ci désigne la section nulle de ![]() , c'est-à-dire l'application
, c'est-à-dire l'application
![]() qui associe à chaque
qui associe à chaque ![]() l'élément nul de de
l'élément nul de de ![]() . Elle est de classe
. Elle est de classe ![]() car son expression locale en coordonnées canoniques est
car son expression locale en coordonnées canoniques est