


suivant: Passage aux composantes et
monter: 4.1 Rappels sur le
précédent: Transposée d'une application linéaire
Table des matières
Lorsque 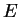 est de dimension finie,
est de dimension finie, 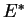 l'est aussi et il existe une liaison naturelle entre les bases de
l'est aussi et il existe une liaison naturelle entre les bases de 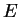 et celles de
et celles de 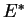 . Soit une base
. Soit une base
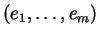 de
de 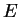 . On pose
Les éléments
. On pose
Les éléments
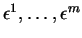 de
de 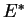 forment une base de
forment une base de 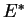 , appelée base duale de la base
, appelée base duale de la base
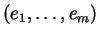 de
de 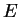 (4.1). En effet, ils engendrent
(4.1). En effet, ils engendrent 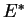 puisque si
puisque si
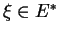 , alors
(Notons au passage que la composante de
, alors
(Notons au passage que la composante de 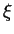 selon
selon
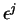 est
est 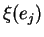 .) Ils sont linéairement indépendants car si
alors
.) Ils sont linéairement indépendants car si
alors
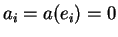 pour tout
pour tout 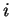 .
.
Soient une base
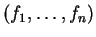 de
de 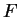 et la base duale associée
et la base duale associée
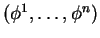 .
Si l'application linéaire
.
Si l'application linéaire 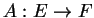 est représentée par la matrice
est représentée par la matrice
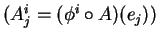 dans les bases
dans les bases
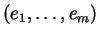 et
et
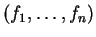 , en sorte que
, en sorte que
alors 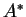 l'est par la matrice transposée dans les bases duales(4.2).
En effet, si
l'est par la matrice transposée dans les bases duales(4.2).
En effet, si
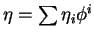 , alors, pour tout
, alors, pour tout 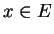 ,
,
2003-11-02
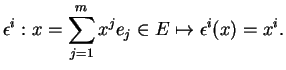
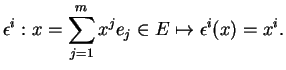
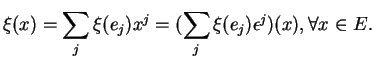
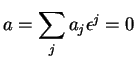
![]() de
de ![]() et la base duale associée
et la base duale associée
![]() .
Si l'application linéaire
.
Si l'application linéaire ![]() est représentée par la matrice
est représentée par la matrice
![]() dans les bases
dans les bases
![]() et
et
![]() , en sorte que
, en sorte que
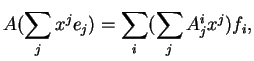
![\begin{displaymath}
% latex2html id marker 13968\begin{array}{rcl}
(A^*(\sum_i...
... [1ex]
&=&(\sum_j(\sum_iA^i_j\eta_i)\epsilon^j)(x).
\end{array}\end{displaymath}](img945.gif)