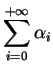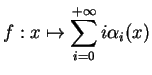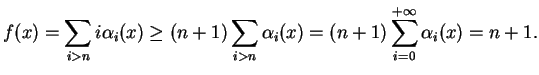


suivant: 2 Le fibré tangent
monter: 1 Variétés différentielles
précédent: 1.3.1.0.7 L'application de Gauss
Table des matières
1.4 L'exercice de Milnor
On appelle ainsi le théorème suivant qui montre à quel point la structure d'une variété différentielle est déterminée par celle de l'algèbre de ses fonctions à valeurs réelles.
Théorème 1.4.1
Soient des variétés différentielles

et
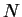
.
Une application linéaire
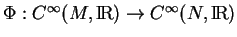
est un isomorphisme d'algèbres(
1.7) si et seulement si il existe un difféomorphisme
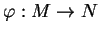
tel que
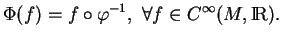 |
(1.2) |
Pour la démonstration de ce théorème, nous aurons besoin de la propositions suivante.
Proposition 1.4.2
Soit une variété différentielle

.
a)Pour tout
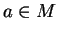
, l'ensemble
est un idéal de
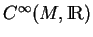
(
1.8).
Il est de codimension
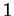
.
b) Si
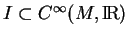
est un idéal de codimension
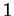
alors il existe
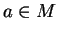
tel que
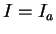
.
c) Si
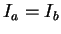
alors
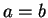
.
Preuve du théorème 4.1. Il est facile de vérifier que les applications 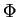 de la forme (2) sont des isomorphismes d'algèbres. Nous allons nous contenter de prouver la réciproque. Soit donc un isomorphisme d'algèbres
de la forme (2) sont des isomorphismes d'algèbres. Nous allons nous contenter de prouver la réciproque. Soit donc un isomorphisme d'algèbres
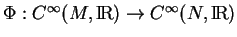 . Il induit une bijection entre les ensembles d'idéaux de codimension
. Il induit une bijection entre les ensembles d'idéaux de codimension 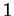 de ces algèbres. D'après la proposition 4.2, il existe donc des applications
de ces algèbres. D'après la proposition 4.2, il existe donc des applications
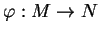 et
et
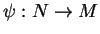 telles que
telles que
et
Il est clair que 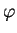 et
et 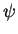 sont des applications réciproques l'une de l'autre. De plus, on a
sont des applications réciproques l'une de l'autre. De plus, on a
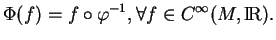 |
(1.3) |
En effet, pour tout  , on peut décomposer une fonction
, on peut décomposer une fonction 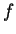 en la somme d'une constante et d'une fonction nulle en
en la somme d'une constante et d'une fonction nulle en  :
En appliquant
:
En appliquant 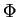 aux deux membres de cette relation puis en évaluant le résultat en
aux deux membres de cette relation puis en évaluant le résultat en
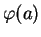 , il vient
car
, il vient
car
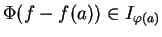 (et
(et
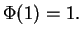 ) Il suffit de remplacer
) Il suffit de remplacer  par
par
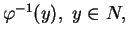 pour obtenir (3).
pour obtenir (3).
Nous devons, pour terminer, montrer que 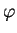 est de classe
est de classe 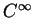 . En remplaçant
. En remplaçant 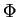 par son inverse, cela suffira pour vérifier que
par son inverse, cela suffira pour vérifier que
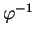 l'est aussi et donc que
l'est aussi et donc que 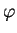 est un difféomorphisme.
est un difféomorphisme.
Commençons par vérifier que 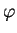 est continu. Soient donc un ouvert non vide
est continu. Soient donc un ouvert non vide 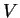 de
de 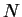 et
et
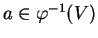 . On peut construire une fonction
. On peut construire une fonction
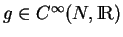 telle que
telle que
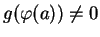 et dont le support soit inclus dans
et dont le support soit inclus dans 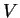 . Posons
. Posons
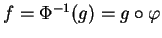 . Si
. Si
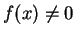 , alors
, alors
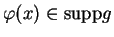 . Par conséquent, l'image par
. Par conséquent, l'image par 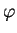 de l'ouvert
de l'ouvert
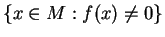 de
de  , qui contient
, qui contient  , est incluse dans
, est incluse dans 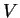 . D'où la continuité de
. D'où la continuité de 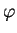 .
.
Soient 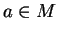 ,
,
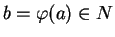 et une carte
et une carte 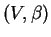 de
de 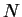 dont le domaine contient
dont le domaine contient 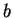 . Quitte à rétrécire
. Quitte à rétrécire 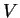 , nous pouvons supposer qu'il existe des fonctions
, nous pouvons supposer qu'il existe des fonctions
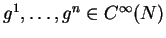 telles que
telles que
Les fonctions
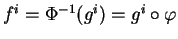 sont de classe
sont de classe 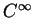 sur
sur  . Soit une carte
. Soit une carte
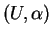 de
de  dont le domaine contient
dont le domaine contient  . Par continuité de
. Par continuité de 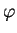 , quitte à restreindre
, quitte à restreindre 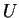 , on peut supposer que
, on peut supposer que
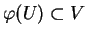 .
Pour
.
Pour 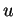 dans
dans 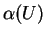 , on a donc
, on a donc
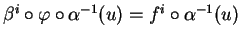 . Par conséquent, l'expression locale
. Par conséquent, l'expression locale
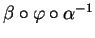 de
de 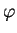 est de classe
est de classe 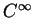 .
.
Preuve de la proposition 4.2. a) Il est clair que 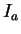 est un idéal. L'application
est un idéal. L'application
étant une bijection entre
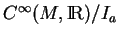 et
et
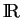 ,
, 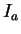 est de codimension
est de codimension 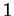 .
.
b) Nous allons prouver b) par l'absurde et, dans ce but, nous admettrons que  possède une fonction propre,
possède une fonction propre, 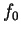 (1.9).
(1.9).
Soit un idéal 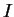 de codimension
de codimension 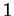 dans
dans
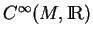 qui ne soit pas de la forme
qui ne soit pas de la forme 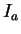 (1.10). Il ne contient pas
(1.10). Il ne contient pas 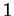 (1.11). Il existe donc
(1.11). Il existe donc
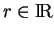 tel que
tel que
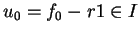 . Puisque
. Puisque 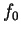 est propre, l'ensemble
est propre, l'ensemble
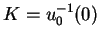 est un compact de
est un compact de  . Comme
. Comme 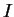 n'est de la forme
n'est de la forme 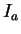 pour aucun
pour aucun  , à chaque point de
, à chaque point de 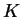 , on peut associer un ouvert qui le contient et un élément de
, on peut associer un ouvert qui le contient et un élément de 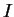 qui ne s'annule pas dans cet ouvert. Par compacité, on peut recouvrir
qui ne s'annule pas dans cet ouvert. Par compacité, on peut recouvrir 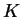 à l'aide d'un nombre fini de ces ouverts: il existe des ouverts
à l'aide d'un nombre fini de ces ouverts: il existe des ouverts
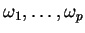 dont l'union contient
dont l'union contient 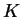 et
et
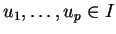 tels que
tels que 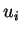 ne s'annule en aucun point de
ne s'annule en aucun point de 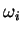 . Posons
. Posons
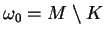 .
La fonction
.
La fonction
est un élément de 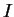 , qui ne s'annule en aucun point. Il en résulte que
, qui ne s'annule en aucun point. Il en résulte que
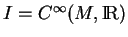 puisque, pour tout
puisque, pour tout
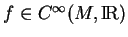 , on a
, on a
Revenons un instant sur l'existence d'une fonction propre.
Appelons partition de l'unité sur  une suite
une suite
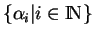 d'éléments de
d'éléments de
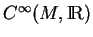 , toutes à valeurs positives, dont les supports forment une famille localement finie de compacts et dont la somme
, toutes à valeurs positives, dont les supports forment une famille localement finie de compacts et dont la somme
converge vers 1. Par définition d'une famille localement finie, pour tout 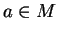 , il existe un ouvert
, il existe un ouvert 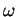 de
de  contenant
contenant  et qui n'est rencontré que par un nombre fini de
et qui n'est rencontré que par un nombre fini de
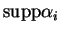 . La série ci-dessus converge donc toujours puisque, sur
. La série ci-dessus converge donc toujours puisque, sur 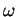 , elle se réduit à une somme finie.
, elle se réduit à une somme finie.
Proposition 1.4.3
Si
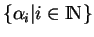
est une partition de l'unité de

, alors
est une fonction propre de

.
Preuve.
La série définissant
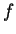
converge vers une fonction différentiable car, de nouveau, c'est localement une somme finie de fonctions différentiables. Cela étant, pour
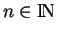
, on a
En effet, si
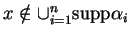
, alors
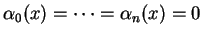
et
Soit alors un compact
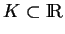
. Il existe un entier
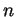
tel que
![$ K\subset]-\infty,n]$](img343.gif)
.
Puisque les valeurs de
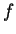
ne sont pas négatives,
Par conséquent,
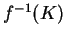
est compact(
1.12).
Nous admettons la propriété suivante.
Proposition 1.4.4
Soit un recouvrement ouvert
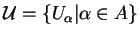
d'une variété

. Il existe une partition de l'unité de

subordonnée à
[ ce qui signifie que le support de chaque élément de la partition est inclus à un des éléments du recouvrement].



suivant: 2 Le fibré tangent
monter: 1 Variétés différentielles
précédent: 1.3.1.0.7 L'application de Gauss
Table des matières
2003-11-02
![]() de la forme (2) sont des isomorphismes d'algèbres. Nous allons nous contenter de prouver la réciproque. Soit donc un isomorphisme d'algèbres
de la forme (2) sont des isomorphismes d'algèbres. Nous allons nous contenter de prouver la réciproque. Soit donc un isomorphisme d'algèbres
![]() . Il induit une bijection entre les ensembles d'idéaux de codimension
. Il induit une bijection entre les ensembles d'idéaux de codimension ![]() de ces algèbres. D'après la proposition 4.2, il existe donc des applications
de ces algèbres. D'après la proposition 4.2, il existe donc des applications
![]() et
et
![]() telles que
telles que
![]() est de classe
est de classe ![]() . En remplaçant
. En remplaçant ![]() par son inverse, cela suffira pour vérifier que
par son inverse, cela suffira pour vérifier que
![]() l'est aussi et donc que
l'est aussi et donc que ![]() est un difféomorphisme.
est un difféomorphisme.
![]() est continu. Soient donc un ouvert non vide
est continu. Soient donc un ouvert non vide ![]() de
de ![]() et
et
![]() . On peut construire une fonction
. On peut construire une fonction
![]() telle que
telle que
![]() et dont le support soit inclus dans
et dont le support soit inclus dans ![]() . Posons
. Posons
![]() . Si
. Si
![]() , alors
, alors
![]() . Par conséquent, l'image par
. Par conséquent, l'image par ![]() de l'ouvert
de l'ouvert
![]() de
de ![]() , qui contient
, qui contient ![]() , est incluse dans
, est incluse dans ![]() . D'où la continuité de
. D'où la continuité de ![]() .
.
![]() ,
,
![]() et une carte
et une carte ![]() de
de ![]() dont le domaine contient
dont le domaine contient ![]() . Quitte à rétrécire
. Quitte à rétrécire ![]() , nous pouvons supposer qu'il existe des fonctions
, nous pouvons supposer qu'il existe des fonctions
![]() telles que
telles que
![]() est un idéal. L'application
est un idéal. L'application
![]() de codimension
de codimension ![]() dans
dans
![]() qui ne soit pas de la forme
qui ne soit pas de la forme ![]() (1.10). Il ne contient pas
(1.10). Il ne contient pas ![]() (1.11). Il existe donc
(1.11). Il existe donc
![]() tel que
tel que
![]() . Puisque
. Puisque ![]() est propre, l'ensemble
est propre, l'ensemble
![]() est un compact de
est un compact de ![]() . Comme
. Comme ![]() n'est de la forme
n'est de la forme ![]() pour aucun
pour aucun ![]() , à chaque point de
, à chaque point de ![]() , on peut associer un ouvert qui le contient et un élément de
, on peut associer un ouvert qui le contient et un élément de ![]() qui ne s'annule pas dans cet ouvert. Par compacité, on peut recouvrir
qui ne s'annule pas dans cet ouvert. Par compacité, on peut recouvrir ![]() à l'aide d'un nombre fini de ces ouverts: il existe des ouverts
à l'aide d'un nombre fini de ces ouverts: il existe des ouverts
![]() dont l'union contient
dont l'union contient ![]() et
et
![]() tels que
tels que ![]() ne s'annule en aucun point de
ne s'annule en aucun point de ![]() . Posons
. Posons
![]() .
La fonction
.
La fonction
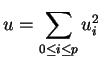
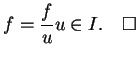
![]() une suite
une suite
![]() d'éléments de
d'éléments de
![]() , toutes à valeurs positives, dont les supports forment une famille localement finie de compacts et dont la somme
, toutes à valeurs positives, dont les supports forment une famille localement finie de compacts et dont la somme