La structure particulière du fibré cotangent donne lieu à un difféomorphisme canonique entre ses propres fibrés tangent et cotangent. Ce difféomorphisme, que nous noterons
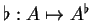 (5.1), respecte la structure vectorielle des espaces tangent et cotangent en ce sens que, pour tout
(5.1), respecte la structure vectorielle des espaces tangent et cotangent en ce sens que, pour tout
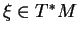 , il se restreint en une bijection linéaire
, il se restreint en une bijection linéaire 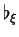 de
de
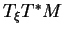 dans
dans
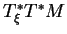 . On dit alors que c'est un isomorphisme- de fibrés vectoriels- entre
. On dit alors que c'est un isomorphisme- de fibrés vectoriels- entre 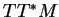 et
et 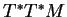 . Nous noterons
. Nous noterons
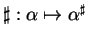 le difféomorphisme inverse(5.2), qui est aussi un isomorphisme puisque
le difféomorphisme inverse(5.2), qui est aussi un isomorphisme puisque
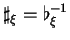 pour tout
pour tout 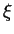 (5.3).
(5.3).
Preuve.
A cause des propriétés
1.1 et
2.3, un tel isomorphisme est forcément unique. Ces mêmes propriétés, qui s'appliquent aussi bien à des domaines de cartes canoniques qu'à
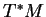
tout entier(
5.4), montrent également que si nous avons construits localement des isomorphismes
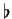
vérifiant (
14) dans des domaines de cartes
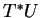
et
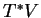
, alors ils coïncident dans l'intersection
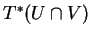
de ceux-ci et se prolongent donc mutuellement dans leur union
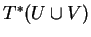
. Il suffit dès lors de construire une solution
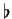
de (
14) dans chaque
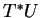
pour conclure. Vu les formules (
12) et (
13), il est clair que l'application
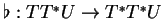
donnée par
lorsque les composantes de
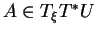
sont
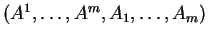
convient. D'où le résultat.
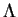
![]() (5.1), respecte la structure vectorielle des espaces tangent et cotangent en ce sens que, pour tout
(5.1), respecte la structure vectorielle des espaces tangent et cotangent en ce sens que, pour tout
![]() , il se restreint en une bijection linéaire
, il se restreint en une bijection linéaire ![]() de
de
![]() dans
dans
![]() . On dit alors que c'est un isomorphisme- de fibrés vectoriels- entre
. On dit alors que c'est un isomorphisme- de fibrés vectoriels- entre ![]() et
et ![]() . Nous noterons
. Nous noterons
![]() le difféomorphisme inverse(5.2), qui est aussi un isomorphisme puisque
le difféomorphisme inverse(5.2), qui est aussi un isomorphisme puisque
![]() pour tout
pour tout ![]() (5.3).
(5.3).
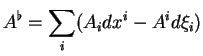
![\begin{displaymath}
% latex2html id marker 14534\begin{array}{rcl}
((X^c)^\fla...
...\\
&=&-[Y,X]\ \tilde{ }\\
&=&-(d\tilde{X})(Y^c)
\end{array}\end{displaymath}](img1083.gif)