


suivant: Un théorème de ``redressement''
monter: 3 Champs de vecteurs
précédent: 3.3 Champs liés
Table des matières
Le crochet de Lie de champs de vecteurs peut être exprimé à l'aide de leurs flots.
Proposition 3.4.1
Soient
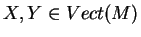
et
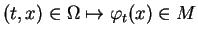
le flot de
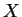
.
Pour tout
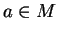
,
Preuve.
i)Vérifions d'abord cette égalité en
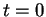
, en coordonnées locales. Pour
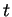
assez proche de 0 et
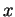
assez proche de

, les points
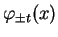
sont dans le domaine d'une carte arbitrairement fixée de

dont le domaine contient

. Notons
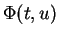
l'expression locale de
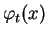
. Celle de
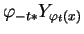
est alors
où
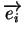
est le
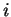
-ième vecteur de la base canonique de
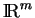
. La dérivée par rapport à
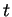
de cette expression comporte trois termes, correspondant aux trois occurrences de
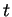
. Pour les calculer, en
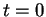
, on utilisera l'égalité
sans oublier que
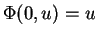
, ce qui entraîne que
Le premier terme vaut ainsi
Le second vaut
Pour le troisième, on obtient
La somme de ces trois termes est bien l'expression locale de
$](img806.gif)
.
ii) Passons maintenant au cas général. Compte tenu de la proposition
2.1 et de i), il vient (
3.9)
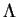
Exemple 3.4.2
![$ [H^*,K^*]=[H,K]^*.$](img810.gif)
En effet, tout champ invariant à gauche étant 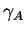 -lié à lui-même pour tout
-lié à lui-même pour tout 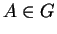 , on a
, on a
Le flot de 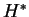 étant donné par
étant donné par
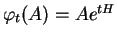 , il vient
D'où la formule annoncée.
, il vient
D'où la formule annoncée.
Lemme 3.4.3
Soient
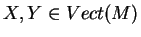
et
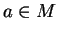
. Notons
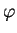
le flot de
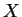
et
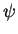
celui de
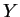
. Il existe un ouvert
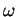
de

contenant

et
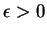
tels que, pour tout
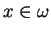
, les fonctions
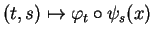
et
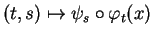
soient définies dans
![$ ]-\epsilon,\epsilon[\times ]-\epsilon,\epsilon[$](img817.gif)
.
Preuve.
Notons
le domaine de définition de
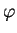
et
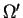
celui de
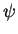
. La fonction
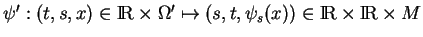
est continue et applique
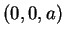
sur lui-même. L'intersection
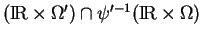
est donc un ouvert non vide, contenant
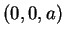
. Il existe donc un ouvert
de

contenant

et
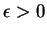
tels que
Autrement dit, l'ensemble
![$ ]-\epsilon,\epsilon[\times ]-\epsilon,\epsilon[\times\omega$](img823.gif)
est donc contenu dans le domaine de définition de
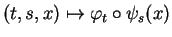
. Quitte à restreindre
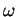
et à diminuer
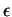
, on peut aussi supposer qu'il l'est dans celui de
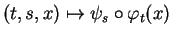
.
Proposition 3.4.4
Soient
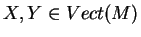
. Notons
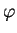
le flot de
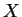
et
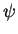
celui de
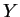
. Si
![$ [X,Y]=0$](img827.gif)
, alors pour tout
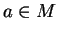
, il existe un ouvert
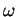
de

contenant

et
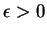
tels que, pour tout
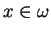
,
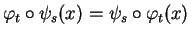 |
(3.5) |
quels que soient
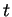
et
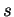
dans
![$ ]-\epsilon,\epsilon[$](img394.gif)
et réciproquement.
Preuve.
Nous choisissons
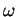
et
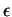
comme dans le lemme ci-dessus.
Supposons que
![$ [X,Y]=0$](img827.gif)
. Pour
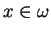
et
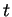
dans
![$ ]-\epsilon,\epsilon[$](img394.gif)
, la dérivée
est nulle. Ainsi,
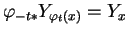
et, dans
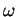
, le champ
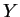
est
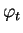
-lié à lui-même. Vu la proposition
3.2, l'égalité (
11) est alors vraie pour tout
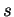
dans
![$ ]-\epsilon,\epsilon[$](img394.gif)
.
Inversement, supposons que les flots de
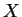
et
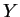
commutent comme indiqué dans l'énoncé. En dérivant l'égalité (
11) par rapport à
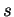
, on obtient
En prenant la dérivée par rapport à
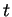
, on constate ensuite que
=0$](img832.gif)
.
Le point

étant arbitraire dans

, on en déduit que le crochet de Lie de
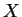
et de
est nul.
Sous-sections



suivant: Un théorème de ``redressement''
monter: 3 Champs de vecteurs
précédent: 3.3 Champs liés
Table des matières
2003-11-02
![$\displaystyle {\frac{d}{dt}{\varphi_{-t*}Y_{\varphi_t(a)}}}=\varphi_{-t*}[X,Y]_{\varphi_t(a)},\forall t\in\Omega_a.
$](img793.gif)
![$\displaystyle {\frac{d}{dt}{\varphi_{-t*}Y_{\varphi_t(a)}}}=\varphi_{-t*}[X,Y]_{\varphi_t(a)},\forall t\in\Omega_a.
$](img793.gif)
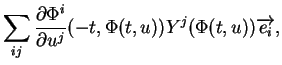
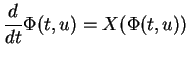
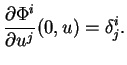
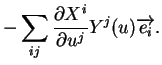
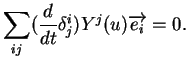
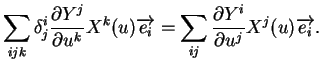
![\begin{displaymath}
% latex2html id marker 13387\begin{array}{rcl}
{\frac{d}{d...
...lambda=0}\\ [1ex]
&=&\varphi_{-s*}Y(\varphi_s(a)).
\end{array}\end{displaymath}](img809.gif)
![]() -lié à lui-même pour tout
-lié à lui-même pour tout ![]() , on a
, on a
![\begin{displaymath}
% latex2html id marker 13402\begin{array}{ccl}
[H^*,K^*]_{...
...dt}{e^{tH}Ke^{-tH}}}_{\vert t=0}\\ [1ex]
&=&HK-KH.
\end{array}\end{displaymath}](img814.gif)
![$\displaystyle {\frac{d}{dt}{\varphi_{-t*}Y_{\varphi_t(x)}}}=\varphi_{-t*}[X,Y]_{\varphi_t(x)}
$](img829.gif)