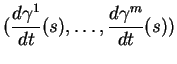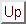


suivant: 2.2 Application linéaire tangente
monter: 2 Le fibré tangent
précédent: 2 Le fibré tangent
Table des matières
Soit une variété  . L'espace tangent à
. L'espace tangent à  en
en  , noté
, noté 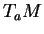 , est, par définition, l'ensemble des
, est, par définition, l'ensemble des  -dérivations de l'algèbre
-dérivations de l'algèbre
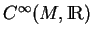 , c'est-à-dire des applications linéaires
, c'est-à-dire des applications linéaires
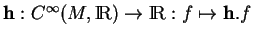 vérifiant
C'est donc un espace vectoriel, sous-espace du dual
vérifiant
C'est donc un espace vectoriel, sous-espace du dual
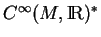 de
de
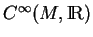 (2.1).
(2.1).
A chaque courbe
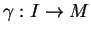 de classe
de classe 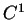 de
de  passant par
passant par  correspond une
correspond une  -dérivation: si
-dérivation: si
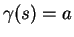 , il s'agit de
, il s'agit de
On l'appelle le vecteur tangent à 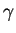 en
en 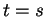 , ou en
, ou en  , s'il est clair que
, s'il est clair que
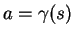 . On le note aussi
. On le note aussi
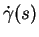 .
.
Théorème 2.1.1
Soient une variété

,
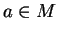
et une carte
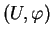
de

dont le domaine contient

.
a) L'espace
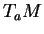
est l'ensemble des vecteurs tangents en

aux courbes de

passant par

.
b) Pour tout
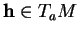
, il existe
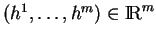
tel que (
2.2)
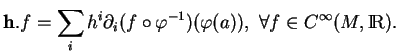 |
(2.1) |
c) L'application
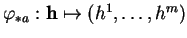
définie par cette relation est une bijection linéaire entre
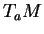
et
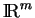
.
La preuve de ce théorème repose sur le lemme suivant.
Lemme 2.1.2
Soient une variété

,
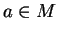
et une carte
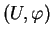
de

dont le domaine contient

. Il existe des fonctions
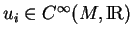
telle que, pour tout
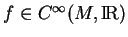
,
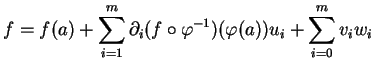 |
(2.2) |
où les fonctions
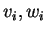
s'annulent en

.
Preuve du théorème 1.1.(i) Appliquons une  -dérivation
-dérivation 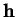 aux deux membres de (5). En tenant compte de ce que
aux deux membres de (5). En tenant compte de ce que
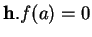 (2.3) et du fait que les fonctions
(2.3) et du fait que les fonctions 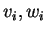 sont nulles en
sont nulles en  , cela donne
Ainsi,
, cela donne
Ainsi, 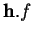 est bien de la forme (4), avec
est bien de la forme (4), avec
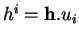 .
.
(ii) En prenant pour 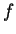 une fonction dont l'expression locale
une fonction dont l'expression locale
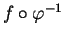 coïncide avec
coïncide avec 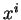 au voisinage de
au voisinage de
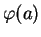 , on voit que
, on voit que
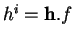 est univoquement déterminé par
est univoquement déterminé par 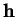 .
En particulier, l'application
.
En particulier, l'application
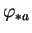 , qui est donnée par
, qui est donnée par
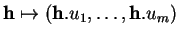 , est bien définie et est linéaire. Elle est visiblement injective.
, est bien définie et est linéaire. Elle est visiblement injective.
(iii) Soit une courbe
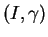 de
de  passant par
passant par  en
en 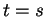 . Quitte à restreindre
. Quitte à restreindre 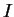 , on peut supposer que
, on peut supposer que
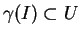 . On a alors
. On a alors
pour tout
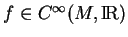 . Soit
. Soit
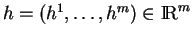 . Pour
. Pour
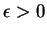 assez petit, la courbe
assez petit, la courbe
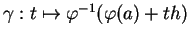 est définie dans
est définie dans
![$ ]-\epsilon,\epsilon[$](img394.gif) , passe par
, passe par  en
en 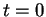 et vérifie
et vérifie
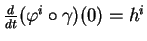 . Avec la relation précédente (où l'on prend
. Avec la relation précédente (où l'on prend 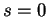 ), ceci démontre a) et prouve que
), ceci démontre a) et prouve que
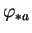 est surjectif.
est surjectif.
Preuve du lemme 1.2. Grâce à la remarque 3.3, on peut trouver des fonctions 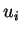 de classe
de classe
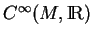 nulle hors de
nulle hors de 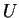 , à support compact dans
, à support compact dans 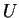 et dont l'expression locale dans la carte
et dont l'expression locale dans la carte
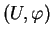 coïncide avec
coïncide avec 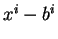 dans un voisinage de
dans un voisinage de
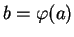 . L'expression locale de la fonction
. L'expression locale de la fonction
s'annule en 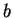 ainsi que ses dérivées premières. Il existe donc des fonctions
ainsi que ses dérivées premières. Il existe donc des fonctions 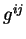 de classe
de classe 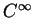 telles que, dans
telles que, dans
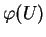 ,
Considérons une fonction
,
Considérons une fonction
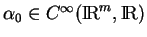 , à valeurs dans
, à valeurs dans ![$ [0,1]$](img146.gif) , à support compact contenu dans
, à support compact contenu dans
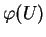 et égale à
et égale à 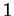 dans un ouvert
dans un ouvert 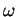 contenant
contenant 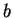 . Notons
. Notons 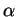 la fonction nulle hors de
la fonction nulle hors de 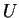 et dont
et dont 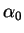 est l'expression locale dans
est l'expression locale dans
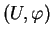 . On a
où
. On a
où
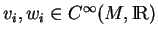 ont
ont
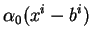
et
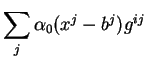
pour expressions locales respectives dans la carte
 .
Il reste à montrer que
.
Il reste à montrer que
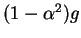 est le produit de deux fonctions nulles en
est le produit de deux fonctions nulles en  .
Pour cela, on prend une fonction
.
Pour cela, on prend une fonction  nulle dans le complémentaire de
nulle dans le complémentaire de 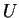 , à valeurs dans
, à valeurs dans ![$ [0,1]$](img146.gif) et dont l'expression locale est à support compact dans
et dont l'expression locale est à support compact dans 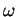 et vaut
et vaut 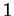 dans un voisinage de
dans un voisinage de 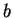 . On peut alors écrire
et prendre
. On peut alors écrire
et prendre
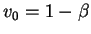 ,
,
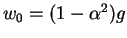 .
.
Avec les notation du théorème précédent, l'élément
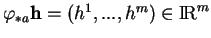 est
l'expression locale de
est
l'expression locale de 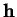 dans la carte
dans la carte
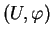 . On voit aussi que l'expression locale de
. On voit aussi que l'expression locale de
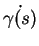 est le vecteur tangent
est le vecteur tangent
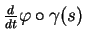 à l'expression locale
à l'expression locale
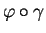 de
de 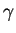 .
.
Remarque 2.1.3
Dans la suite, nous identifierons l'espace tangent
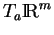
à
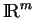
en chaque point

avec
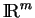
, en confondant la

-dérivation
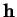
d'expression locale
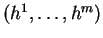
dans la carte canonique
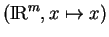
avec
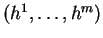
.
Vu comme  -dérivation, ce dernier est donc l'application
-dérivation, ce dernier est donc l'application
Dans l'identification ci-dessus, le vecteur tangent
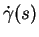 à une courbe
à une courbe
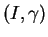 de
de
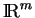 au sens de la définition donnée plus haut est confondu avec
au sens de la définition donnée plus haut est confondu avec
lequel correspond à la définition du vecteur tangent à une courbe donnée dans des cours antérieurs.



suivant: 2.2 Application linéaire tangente
monter: 2 Le fibré tangent
précédent: 2 Le fibré tangent
Table des matières
2003-11-02
![]() de classe
de classe ![]() de
de ![]() passant par
passant par ![]() correspond une
correspond une ![]() -dérivation: si
-dérivation: si
![]() , il s'agit de
, il s'agit de
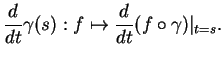
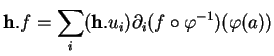
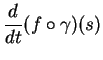
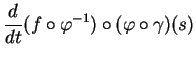
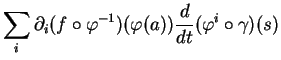
![]() de classe
de classe
![]() nulle hors de
nulle hors de ![]() , à support compact dans
, à support compact dans ![]() et dont l'expression locale dans la carte
et dont l'expression locale dans la carte
![]() coïncide avec
coïncide avec ![]() dans un voisinage de
dans un voisinage de
![]() . L'expression locale de la fonction
. L'expression locale de la fonction
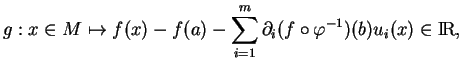
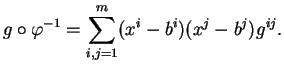
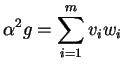
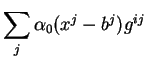
![]() est
l'expression locale de
est
l'expression locale de ![]() dans la carte
dans la carte
![]() . On voit aussi que l'expression locale de
. On voit aussi que l'expression locale de
![]() est le vecteur tangent
est le vecteur tangent
![]() à l'expression locale
à l'expression locale
![]() de
de ![]() .
.
![]() -dérivation, ce dernier est donc l'application
-dérivation, ce dernier est donc l'application
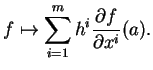
![]() à une courbe
à une courbe
![]() de
de
![]() au sens de la définition donnée plus haut est confondu avec
au sens de la définition donnée plus haut est confondu avec