
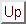


suivant: 3.3 Champs liés
monter: 3.2 Courbes intégrales et
précédent: 3.2 Courbes intégrales et
Table des matières
On garde les mêmes notations.
Proposition 3.2.3
Soit une courbe
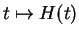
de
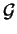
, définie et de classe
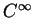
dans l'intervalle
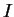
.
Pour tout
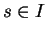
et tout
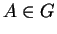
, il existe une seule courbe
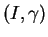
de
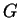
telle que
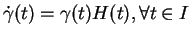 |
(3.4) |
et
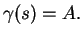
Preuve.
i)
Pour tout 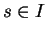 et tout
et tout 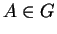 , il existe
, il existe
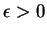 et un ouvert
et un ouvert 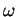 de
de 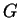 contenant
contenant 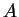 tels que, pour tout
tels que, pour tout
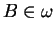 , l'équation (10) admet une seule solution dans
, l'équation (10) admet une seule solution dans
![$ ]s-\epsilon,s+\epsilon[$](img696.gif) passant par
passant par 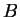 en
en 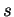 .
.
Pour vérifier ceci, on exprime l'équation donnée en coordonnées locales. On applique alors les propriétés des systèmes d'équations différentielles ordinaires à l'équation obtenue pour conclure. De façon plus détaillée, soient des cartes
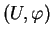
et
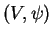
de
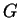
telles que
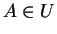
et
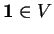
. La multiplication étant continue, quitte à rétrécire
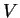
, on peut choisir un ouvert
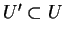
, contenant
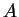
et tel que
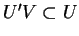
. Notons
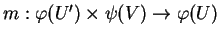
l'expression locale de la multiplication de
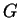
,
et, pour chaque
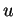
, désignons par
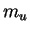
l'application partielle
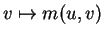
exprimant en coordonnées locales la multiplication à gauche par
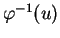
.
Notons également
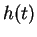
l'expression locale
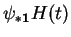
de
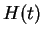
.
Dans les coordonnées locales choisies, l'équation proposée s'écrit
C'est bien un système d'équations différentielles ordinaires, comme annoncé. D'où i).
ii)
Si
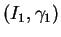 et
et
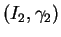 vérifient tous les deux l'équation (10) et si
vérifient tous les deux l'équation (10) et si
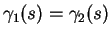 pour un certain
pour un certain
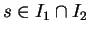 , alors
, alors 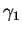 et
et 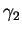 sont égaux dans
sont égaux dans
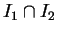 .
.
Montrons que l'ensemble
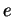
des
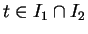
en lesquels
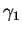
et
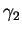
sont égaux est à la fois ouvert et fermé. Comme il n'est pas vide et comme
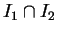
est connexe, il en résultera que
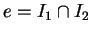
. Les fonctions
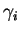
étant continues, il est clair que
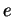
est fermé (car

est séparé). Le fait que
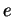
soit ouvert est une conséquence immédiate de i). D'où ii).
iii)
Pour tout 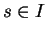 , l'équation (10) admet une solution maximale
, l'équation (10) admet une solution maximale
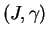 , et une seule, passant par
, et une seule, passant par 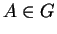 en
en 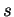 .
. L'unicité est immédiate. Vérifions l'existence. D'après i), il existe au moins une solution à l'équation proposée. D'après ii), deux solutions coïncident dans l'intersection de leurs domaines de définitions et se prolongent donc mutuellement dans l'union de ceux-ci. La solution maximale est celle que l'on obtient en prolongeant toutes les solutions à l'union de leurs domaines de définition.
iv)
Si
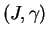 est une solution de (10), alors, pour tout
est une solution de (10), alors, pour tout 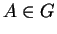 ,
,
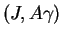 en est une aussi.
en est une aussi. C'est immédiat.
v)
Le domaine de la solution maximale
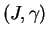 coïncide avec
coïncide avec 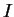 .
. Supposons par exemple que
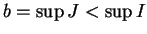
. Vu i), il existe une solution
![$ (]b-\epsilon,b+\epsilon [,U)$](img724.gif)
de l'équation
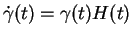
qui passe par
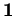
en
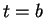
. La courbe
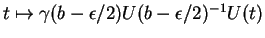
est solution de la même équation et passe par
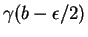
en
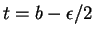
. Vu ii), elle prolonge donc
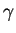
au-delà de
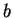
, ce qui est absurde. Donc
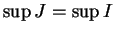
. On démontre de manière analogue que
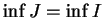
.
En prenant 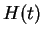 constant dans la proposition 2.3, on obtient le flot des champs invariants à gauche de
constant dans la proposition 2.3, on obtient le flot des champs invariants à gauche de 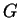 comme décrit plus haut.
comme décrit plus haut.
Voici une autre application de cette proposition.
Proposition 3.2.4
Soient des fonctions
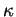
et
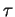
définies sur un intervalle
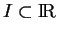
, où elles sont de classe
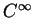
(
3.7), les valeurs de
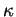
étant positives. Il existe un arc régulier de courbe
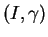
de
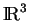
dont
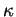
et
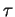
soient la courbure et la torsion respectivement. Cet arc est unique à isométrie positive près.
Preuve.
Notons
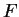
la fonction associant à
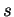
la matrice ayant pour colonnes les composantes de la tangente unitaire
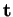
, de la normale principale
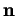
et de la binormale
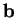
d'un arc régulier de courbe rapporté à une abscisse curviligne
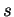
. Elle prend ses valeurs dans le groupe
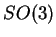
des matrices orthogonales de déterminant
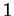
car le trièdre de Frenet est, en tout point de l'arc, une base orthonormée positive. Les équations de Frenet s'écrivent
où
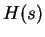
est la matrice
Celle-ci est une courbe de l'espace des matrices antisymétriques, qui est l'algèbre de Lie
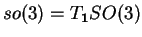
. Les fonctions
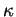
et
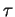
étant données, il résulte donc de la proposition
2.3 qu'il existe une solution
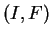
de l'équation ci-dessus et qu'elle est déterminée par sa valeur en un point de
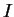
, c'est-à-dire, à une rotation près. Une primitive de la première colonne
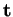
de
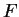
donne un arc régulier de courbe répondant à la question. Chaque composante de la primitive étant définie à une constante près, cet arc est, en fin de compte, déterminé à un déplacement près.
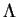
Reprenons l'exemple 3.5 des homographies 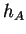 associées aux éléments
associées aux éléments 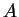 de
de
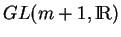 . Lorsqu'on prend
. Lorsqu'on prend
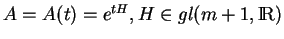 , et
, et
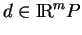 , on obtient une courbe
, on obtient une courbe
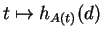 de
de
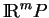 . On définit alors un champ de vecteurs
. On définit alors un champ de vecteurs 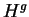 de
de
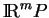 en posant
en posant
Pour écrire l'expression locale de ce champ dans la carte
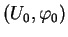 , découpons la matrice
, découpons la matrice 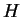 en isolant la première ligne et la première colonne:
où
en isolant la première ligne et la première colonne:
où
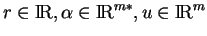 et
et
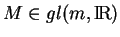 .
En notant
.
En notant 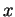 les coordonnées locales
les coordonnées locales
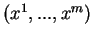 , il est facile de vérifier que l'expression locale de
, il est facile de vérifier que l'expression locale de 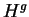 est
(Les expressions locales dans les autres cartes canoniques de
est
(Les expressions locales dans les autres cartes canoniques de
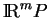 sont analogues.)
Le champ
sont analogues.)
Le champ 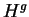 est donc bien de classe
est donc bien de classe 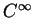 . Son flot est l'application
En effet,
. Son flot est l'application
En effet,
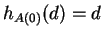 et, puisque
et, puisque
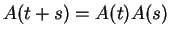 ,
Les courbes intégrales maximales de
,
Les courbes intégrales maximales de 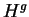 sont donc définies sur
sont donc définies sur
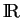 tout entier(3.8)
tout entier(3.8)
Ce n'est pas toujours le cas des solutions des équations différentielles dont leurs expressions locales sont solutions dans les cartes de
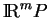 . Par exemple, avec
. Par exemple, avec 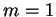 et
et
il s'agit de l'équation différentielle
dans la carte
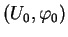 et de
et de
dans la carte
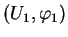 . La solution de la première est
. La solution de la première est
Quand 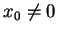 , elle n'est pas définie sur tout
, elle n'est pas définie sur tout
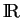 alors que les solutions
alors que les solutions 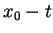 de la seconde sont toutes définies sur
de la seconde sont toutes définies sur
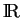 .
Naturellement, le changement de cartes
.
Naturellement, le changement de cartes
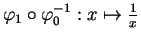 fait passer de l'une à l'autre.
fait passer de l'une à l'autre.



suivant: 3.3 Champs liés
monter: 3.2 Courbes intégrales et
précédent: 3.2 Courbes intégrales et
Table des matières
2003-11-02
![]() constant dans la proposition 2.3, on obtient le flot des champs invariants à gauche de
constant dans la proposition 2.3, on obtient le flot des champs invariants à gauche de ![]() comme décrit plus haut.
comme décrit plus haut.
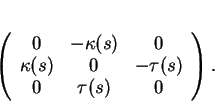
![]() associées aux éléments
associées aux éléments ![]() de
de
![]() . Lorsqu'on prend
. Lorsqu'on prend
![]() , et
, et
![]() , on obtient une courbe
, on obtient une courbe
![]() de
de
![]() . On définit alors un champ de vecteurs
. On définit alors un champ de vecteurs ![]() de
de
![]() en posant
en posant
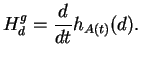
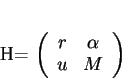
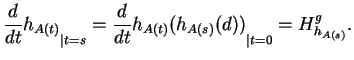
. Par exemple, avec
et
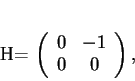
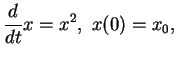
et de
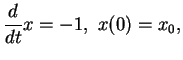
. La solution de la première est
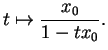
, elle n'est pas définie sur tout
alors que les solutions
de la seconde sont toutes définies sur
. Naturellement, le changement de cartes
fait passer de l'une à l'autre.