4.2 Le fibré $T^*M$

Pour tout $a\in M$, on note $T^*_aM$ le dual de $T_aM$ et on pose

$$T^*M=\bigcup_{x\in M}T^*_xM.$$

Le danger de confusion avec son homologe introduit à propos du fibré tangent étant négligeable, on note encore $\pi_M$ l'application associant $x$ à $\xi\in T^*_xM$.

Proposition 4.2.1   Si $(U,\varphi)$ est une carte de $M$, alors $(TU,(\varphi,\varphi^{-1*}))$, où

$$(\varphi,\varphi^{-1*}): \xi\in T_aM\mapsto (\varphi(a),(\varphi^{-1}_*)^*\xi)\in \varphi(U)\times{\rm I\!R}^{m*},$$

est une carte de $T^*M$. Les cartes de $T^*M$ de cette forme sont toutes compatibles. Elles définissent une structure de variété sur $T^*M$, de dimension $2\dim M$, pour laquelle $\pi_M$ est de classe $C^\infty$ et est une submersion.

Preuve. Explicitons l'application $\varphi^{-1*}$. Soient $a\in U$, $u=\varphi(a)$, $\xi\in T^*_aM$ et $(h^1,\ldots,h^m)\in{\rm I\!R}^m$. Vu la remarque 1.1,

$$(\varphi^{-1*}(\xi))((h^1,\ldots,h^m)=\sum_ih^i\xi(\partial_i(a)).$$

En particulier,

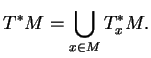
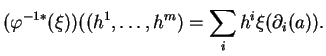
$\varphi^{-1*}$ transforme $T^*_aM$ en ${\rm I\!R}^{m*}$ et la base duale de $(\partial_1(a),\ldots,\partial_m(a))$ de $T^*_aM$ en la base duale de la base canonique de ${\rm I\!R}^m$.

Il alors clair que $(\varphi,\varphi^{-1*})$ est une bijection de $T^*U$ sur $\varphi(U)\times{\rm I\!R}^{m*}$.

Soit une carte $(V,\psi)$ de $M$. Examinons le changement de cartes $(\psi,\psi^{-1})\circ(\varphi,\varphi^{-1*})^{-1}$. Si $U\cap V\neq\emptyset$, alors $T^*U\cap T^*V=T^*(U\cap V)\neq \emptyset$ et

$$(\psi,\psi^{-1})\circ(\varphi,\varphi^{-1*})^{-1}=(\psi\circ\varphi^{-1},((\varphi\circ\psi^{-1})_*)^*)$$

est une bijection de classe $C^\infty$ entre $\varphi(U\cap V)\times{\rm I\!R}^{m*}$ et $\psi(U\cap V)\times{\rm I\!R}^{m*}$. Ces cartes sont donc compatibles. Enfin, l'expression locale

$$\varphi\circ\pi_M\circ(\varphi,\varphi^{-1*})^{-1}:(u,h)\mapsto u.$$

de $\pi_M$ dans les cartes $(U,\varphi)$ et $(TU,(\varphi,\varphi^{-1*}))$ est une application linéaire surjective. Sa différentielle l'est donc aussi. $\qedsymbol$

Les cartes de $T^*M$ de la forme $(TU,(\varphi,\varphi^{-1*}))$ seront dites canoniques.

Afin d'éviter toute confusion, nous ne devrions pas utiliser la notation $\partial_i$ pour désigner la base locale des vecteurs tangents associée à une telle carte comme nous en avions pris l'habitude pour une carte quelconque de $M$. En effet, $\partial_i$ est une abréviation de $\frac{\partial}{\partial x^i}$. Or, il y a $2m$ coordonnées locales relatives à une carte canonique, les $x^i$ mais aussi les $\xi_i$ et ce que $\partial_i$ désignerait ne serait donc pas clair: la dérivée partielle par rapport à $x^i$ ou celle par rapport à $\xi_i$. Une convention supplémentaire commode permet de lever cette ambiguité: nous désignerons encore $\frac{\partial}{\partial x^i}$ par $\partial_i$ tandis que nous désignerons $\frac{\partial}{\partial\xi_j}$ par $\overline{\partial}_j$.