


suivant: 3.4.1.0.3 Champs de vecteurs
monter: 3.4.1 compléments
précédent: 3.4.1.0.1 Champs de vecteurs
Table des matières
On conserve les notations du paragraphe précédent. Montrer que pour tout
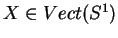 , il existe un ouvert
, il existe un ouvert 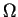 contenant
contenant 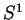 et une fonction
et une fonction
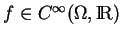 tels que
tels que 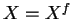 .
.
2003-11-02