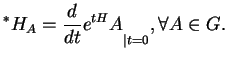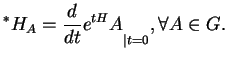


suivant: 3.4.1.0.6 Champs invariants à
monter: 3.4.1 compléments
précédent: 3.4.1.0.4 Champs de vecteurs
Table des matières
Soit un sous groupe 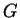 de
de
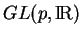 qui en soit une sous-variété plongée. Pour
qui en soit une sous-variété plongée. Pour
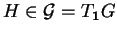 , on pose
Montrer que les champs de vecteurs
, on pose
Montrer que les champs de vecteurs 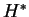 et
et 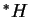 sont
sont 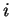 -liés, où
-liés, où
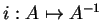 est le passage à l'inverse. En déduire
est le passage à l'inverse. En déduire ![$ [^*H,^*K]$](img911.gif) en fonction de
en fonction de ![$ [H,K]$](img912.gif) .
.
2003-11-02