Preuve.
En effet, si
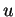
est une fonction de classe
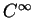
arbitraire sur
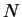
, alors, il vient successivement
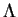
Proposition 3.3.2
Soient des champs
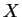
et
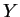
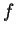
-liés.
a) Si
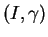
est une courbe intégrale de
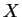
alors
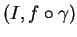
en est une de
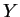
.
b) En particulier, si la courbe intégrale maximale
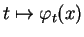
passant par
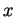
en 0 de
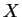
est définie dans
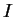
, alors la courbe intégrale maximale
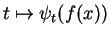
de
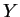
passant par
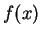
en 0 est définie au moins dans
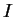
et
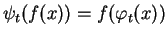
pour tout
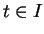
.
![\begin{displaymath}
% latex2html id marker 13271\begin{array}{rcl}
([Y,Y']\cir...
... f))\\
&=&[X,X'].(u\circ f)\\
&=&(f_*[X,X']).u.
\end{array}\end{displaymath}](img785.gif)