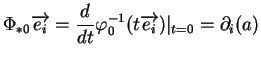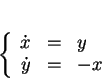Proposition 3.4.5
Soient
et des champs de vecteurs
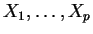
dont les commutateurs
![$ [X_i,X_j]$](img834.gif)
soient tous nuls. Si les vecteurs tangents
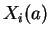
sont linéairement indépendants, alors il existe une carte
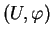
de

dont le domaine contient

et dans laquelle
Preuve.
Désignons par
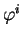
le flot de
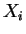
. En vertu d'une généralisation facile du lemme
4.3, il existe un ouvert
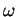
de

contenant

et un nombre positif
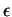
tels que
existe pour tous
![$ t^1,\ldots,t^p\in]-\epsilon,\epsilon[$](img840.gif)
et tout
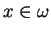
. Choisissons une carte
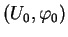
de

dont le domaine contient

telle que
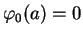
et
On obtient une telle carte à partir d'une carte quelconque composée avec une affinité qui translate l'image de

en 0 et qui transforme les expressions locales des
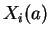
en les
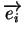
.
Posons
L'application
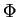
est de classe
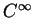
dans un voisinage ouvert de 0 dans
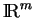
. Nous allons vérifier que
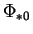
est non singulier et que
En vertu du théorème de la fonction inverse, la première propriété montre que
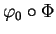
est un changement de variables au voisinage de 0 et que, par conséquent, en rétrécissant
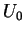
à un ouvert contenant

assez petit, on obtient une carte
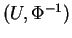
de

. Elle nécessite seulement que les champs considérés soient indépendants en

.
La seconde propriété montre que cette carte répond à la question. Elle utilise le fait que les champs
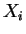
commutent.
Vérifions ces propriétés.
Par définition,
Si 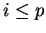 alors
alors
car les applications
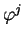
commutent puisque les crochets
![$ [X_j,X_k]$](img854.gif)
sont nuls deux à deux.
En particulier,
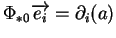
.
Si 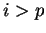 , alors
, alors
car
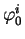
est l'identité dans
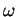
. Donc
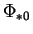
transforme la base des
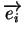
de
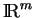
en la base des
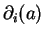
de
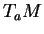
. Il est donc non singulier.
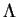
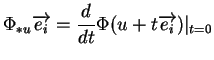
![]() alors
alors
![\begin{displaymath}
% latex2html id marker 13642\begin{array}{rcl}
\Phi_{*u}\o...
...ts,0,u^{p+1},\ldots,u^m)}}\\ [1ex]
&=&X_i(\Phi(u))
\end{array}\end{displaymath}](img852.gif)
![]() , alors
, alors