


suivant: 3.4.1.0.5 Champs invariants à
monter: 3.4.1 compléments
précédent: 3.4.1.0.3 Champs de vecteurs
Table des matières
Soit une base 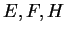 de l'algèbre de Lie
de l'algèbre de Lie 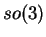 .
.
a)Montrer que pour tout
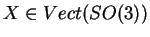 , il existe des fonctions
, il existe des fonctions
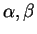 et
et 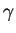 de classe
de classe 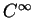 sur un voisinage ouvert de
sur un voisinage ouvert de 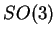 dans
dans
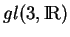 telles que
b)Calculer le crochet de Lie
telles que
b)Calculer le crochet de Lie
![$ [X^{\alpha,\beta,\gamma},X^{\alpha',\beta',\gamma'}]$](img900.gif) sous la forme
sous la forme
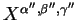
c)En identifiant
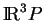 à
à 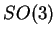 (3.1), pour
(3.1), pour
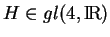 déterminer des fonctions
déterminer des fonctions
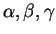 telles que
telles que
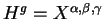 .
.
2003-11-02