6.1.5.6 Le théorème de Clairaut

Soit une courbe $(J,\gamma)$ tracée sur $\Sigma$. Pour tout $t\in J$, on note $d(t)$ la distance de $\gamma(t)$ à l'axe de révolution et $\alpha(t)$ l'angle que font les tangentes en $\gamma(t)$ à $\gamma$ et au méridien de $\Sigma$ passant par $\gamma(t)$.

Théorème 41   (Clairaut) Si $(J,\gamma)$ est une géodésique de $\Sigma$, alors $d(t)\sin\alpha(t)$ est constant. Réciproquement, une courbe $(J,\gamma)$ tracée sur $\Sigma$ et telle que $d(t)\sin\alpha(t)$ soit constant est une géodésique pour autant qu'il n'y ait pas d'intervalle ouvert $J'\subset J$ tel que $\gamma (J')$ soit contenu dans un parallèle.

Tout revient à examiner à quelles conditions la dérivée de $t\mapsto d(t)\sin\alpha(t)$ est nulle dans l'intervalle de définition d'une courbe $(J,\gamma)$ de $\Sigma$. La question étant locale, nous pouvons supposer que $\gamma$ s'écrit

$$t\mapsto \varphi(u(t),v(t))$$

pour un paramétrage $(U,\varphi)$ de la forme (14) et qu'il est paramétré par une abscisse curviligne. En particulier, $\vert\gamma'\vert=1$. Ainsi

$$\cos\alpha=\frac{\gamma'.\partial_v\varphi}{\vert\gamma'\vert\vert\partial_v\varphi\vert} =v'\sqrt{1+r'^2}$$

Dès lors, compte tenu de (16),

$$d^2\sin^2\alpha=r^2(1-\cos^2\alpha)=r^4u'^2$$

Il vient ainsi

$$(d^2\sin^2\alpha)'=2r^4u'(u''+\frac{2r'}{r}u'v')$$

Cela posé, si $(J,\gamma)$ est une géodésique, alors, vu (15), la dérivée de $d\sin\alpha$ est nulle. Réciproquement, si cette dérivée est nulle alors

$$u''+\frac{2r'}{r}u'v'=0$$

C'est immédiat en les points en lesquels $u'\neq 0$ ou qui sont limite de tels points et s'est également vrai dans les ouverts où $u'=0$. De plus, en dérivant (16), on obtient alors

$$v'(v''-\frac{rr'}{1+r'^2}u'^2+\frac{r'r''}{1+r'^2}v'^2)=0$$

Donc, s'il n'existe pas d'intervalle ouvert dans lequel $v'=0$, alors la seconde équation de (15) est également satisfaite et $(J,\gamma)$ est une géodésique.$\qedsymbol$

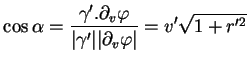
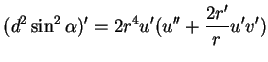
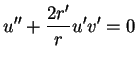
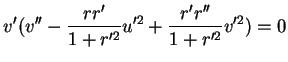
Le long d'un parallèle, $d$ est constant, de même que $\alpha=\frac \pi 2$. On a vu plus haut que les seuls parallèles qui sont des géodésiques sont ceux pour lesquels $r$ est stationnaire. La quantité $d\sin\alpha$ peut donc bien être constante le long d'une courbe qui ne soit pas une géodésique.